Light Field Compression with Homography-based Low Rank Approximation

X. Jiang, M. Le Pendu, R. Farrugia, C. Guillemot,
"Light Field Compression with Homography-based Low Rank Approximation", IEEE Journal of Selected Topics in Signal Processing (J-STSP), vol. 11, No. 7, pp. 1132-1145, Oct. 2017.(pdf)

contact: X. Jiang, M. Le Pendu, C. Guillemot

Abstract

This paper describes a light field compression scheme based on a novel homography-based low rank approximation method called HLRA. The HLRA method jointly searches for the set of homographies best aligning the light field views and for the low rank approximation matrices. The light field views are aligned using either one global homography or multiple homographies depending on how much the disparity across views varies from one depth plane to the other. The light field low-rank representation is then compressed using HEVC. The best pair of rank and QP parameters of the coding scheme, for a given target bit-rate, is predicted with a model defined as a function of light field disparity and texture features. The results are compared with those obtained by directly applying HEVC on the light field views re-structured as a pseudo-video sequence. The experiments using different data sets show substantial PSNR-rate gain of our compression algorithm, as well as the accuracy of the proposed parameter prediction model, especially for real light fields. A scalable extension of the coding scheme is finally proposed.

Datasets

In this work, we consider real light fields captured by plenoptic cameras using an array of micro-lenses, coming from different sources: 1/- INRIA dataset which contains LFs captured either by a first generation Lytro camera (11 × 11 views of 379 × 379 pixels) and a second generation Lytro Illum camera (15 × 15 views of 625 × 434 pixels); 2/- the ICME 2016 Grand Challenge dataset containing 12 Lytro Illum LFs, and we take 13 × 13 central views as defined by the challenge testing conditions.

The complete INRIA dataset can be accessed [ here ...]. It contains 63 LFs captured by Lytro first generation camera and 43 LFs captured by Lytro Illum camera). 4 Lytro 1G LFs ("TotoroWaterfall", "Beers", "Flower" and "TapeMeasure") and 4 Lytro Illum LFs ("Fruits", "Bench", "BouquetFlower1" and "Toys") are used for testing in this paper. The rest of the LFs are used for training the Random Forest based parameter prediction model (c.f. Section "Model-based coding parameters prediction"). We only consider the 9 × 9 central sub-aperture images in order to alleviate the strong vignetting and distortion problems on the views at the periphery of the light field which comparatively more several impacts the performance of the HEVC-based reference schemes. Note that there are still variations of light intensity, but to a lesser extent, in the truncated light fields.

Lytro LFs are decoded by the Matlab Light Field Toolbox v0.4.

Homography-based low rank approximation

Our low rank approximation methods exploit data geometry for dimensionality reduction of light fields. We consider the coding of the sub-aperture images (i.e. views) already extracted from a lenslet image. Thanks to the high correlation between the views in such light fields, the matrix whose columns are formed by vectorizing each view can be well approximated by a low rank matrix. In addition, a prior alignment of the views with homography warpings increases the correlation and thus improves the low rank approximation.

In the proposed method, homographies and the rank approximation model are jointly optimized. Homography projections are searched for each view in order to obtain the best low rank matrix approximation for a given target rank k (where k is less than the number of views). The rank constraint is expressed in a factored form where one matrix B contains k basis vectors and where the other one C contains weighting coefficients. The optimization hence proceeds by iteratively searching for the homographies and the factored model of the input set of sub-aperture images, which will minimize the approximation error.

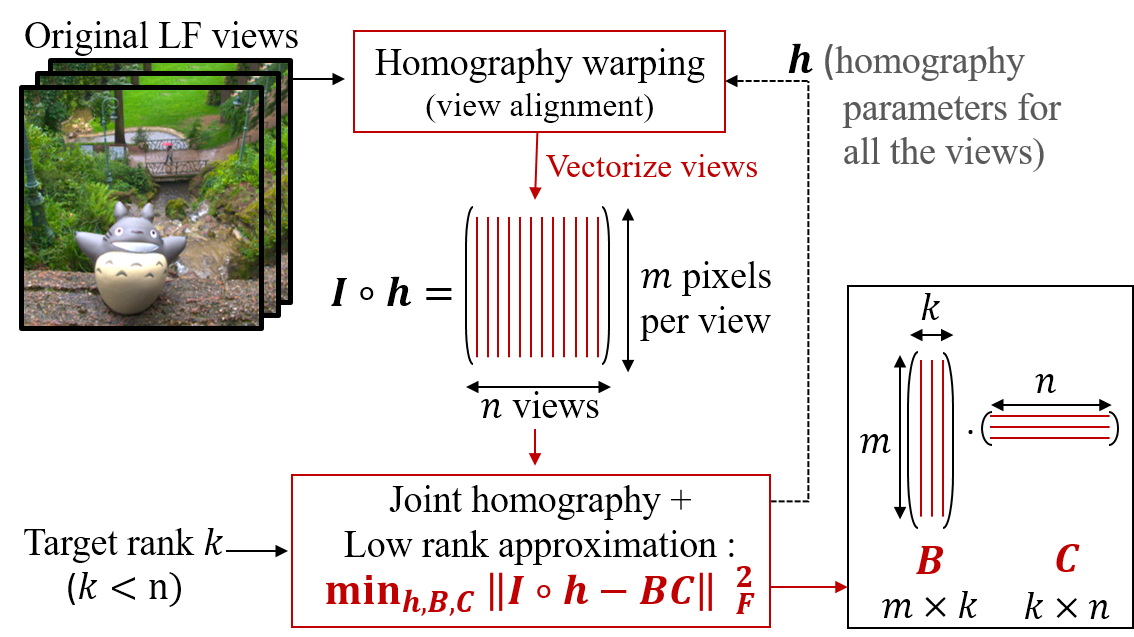
Depth-based multiple homographies

When the disparity varies from one depth plane to another, one global homography per view is not sufficient to well align the whole views. For such light fields, the homography-based low rank approximation method can be extended to the case where different homographies are computed for different depth planes segmented thanks to a scene depth map. Depth map D can be normalized between 0 and 1. Depth planes is then obtained by uniformly quantizing the depth map with a series of quantization thresholds. The thresholds are defined to split in equal parts the range of depth values between the minimum and maximum depth in D. To cope with artifacts at the frontier of two depth planes when performing the homography warpings, instead of blending the pixel values, a blending of homographies is performed.

TotoroWaterfalll: separation into 2 depth planes

Compression details

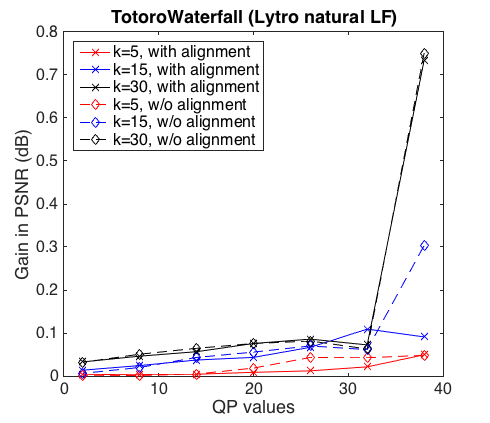
The columns of the matrix B are first quantized on 16 bits before being encoded using HEVC-Intra coding. However, any encoder could be used to compress the proposed homography-based low rank representation.
The following figure shows the first 3 columns of B when HLRA is applied for the LF "TotoroWaterfall" with rank k = 5 and 1 homography per image. The first column represents low frequency information, whereas the others contain data with high frequency. One can observe that by using homographies to align sub-aperture views, the average image in the first column becomes sharper, and there is less high frequency information remaining in the following columns.

Columns of matrix B without alignment.

Columns of matrix B with alignment: k = 5, q = 1.

Since the matrix B will need to be compressed to be transmitted to the receiver side, in order to reduce the impact of the compression (i.e. quantization) errors on the light field reconstruction, the matrix C is recalculated to account for these quantization errors. Following figures show the the PSNR gain when we adapt C to the compression artifacts of the matrix B.

Besides the matrix B, additional elements need to be transmitted. The coefficients of the matrix C are encoded using a scalar quantization on 16 bits and Huffman coding. The 8 × n × q homography parameters, with q the number of depth planes per view, are encoded the same way. In the case where multiple homograhies are applied, the depth map is encoded using HEVC intra coding with QP = 32.

Model-based coding parameters prediction

Problem

For a given target bit-rate and a given input light field, the PSNR performance of the compression scheme depends on two key parameters: the rank k of the approximation and the HEVC quantization parameter (QP). The (k, QP) prediction task can be considered as a problem of Multi-output classification (MOC).

Training and Test LFs

c.f. Section "Datasets".

Input Feature space

Disparity indicators of original light field:

proportion of singular values of the matrix I which contain at least 95% of the energy of I;
decay rate of singular values of the matrix I which is defined as the ratio between the first and the second singular value.

Disparity indicators of aligned light field: same indicators as above computed on the aligned LF.
Texture indicators: same indicators as above computed on the matrix in which each column is a vectorized version of each 8 × 8 block of the central view.
Bitrate of the encoded light field for a certain pair (k, QP)
Target bitrate

Prediction model

We use Random Forest as classifier. For MOC problems, a classical way is to predict separately each label with a different classifier by assuming that these labels are independent. In our case, however, k and QP are strongly correlated. In order to improve the MOC performance, we model the label dependencies by a competitive Classifier Chain (CC). In such a scheme, the values of k and QP are at first separately predicted by two independent Random Forests. We then choose the prediction (k or QP) for which the classifier gets a higher probability and add it into the new feature space. A third Random Forest is then employed to predict the other label with the augmented feature space.

Results

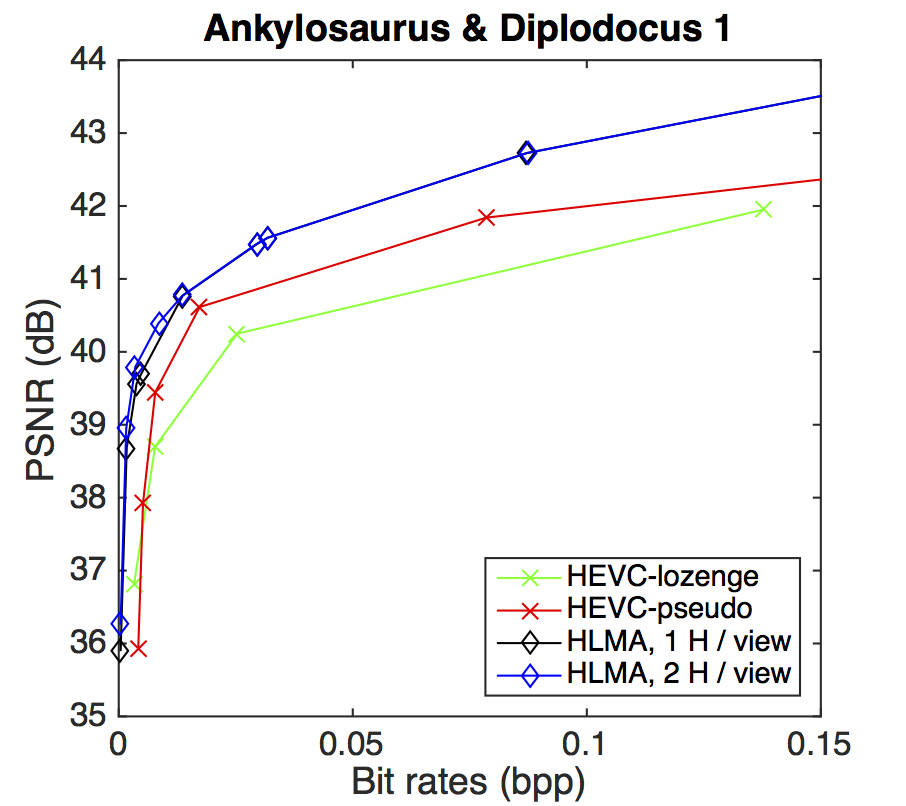
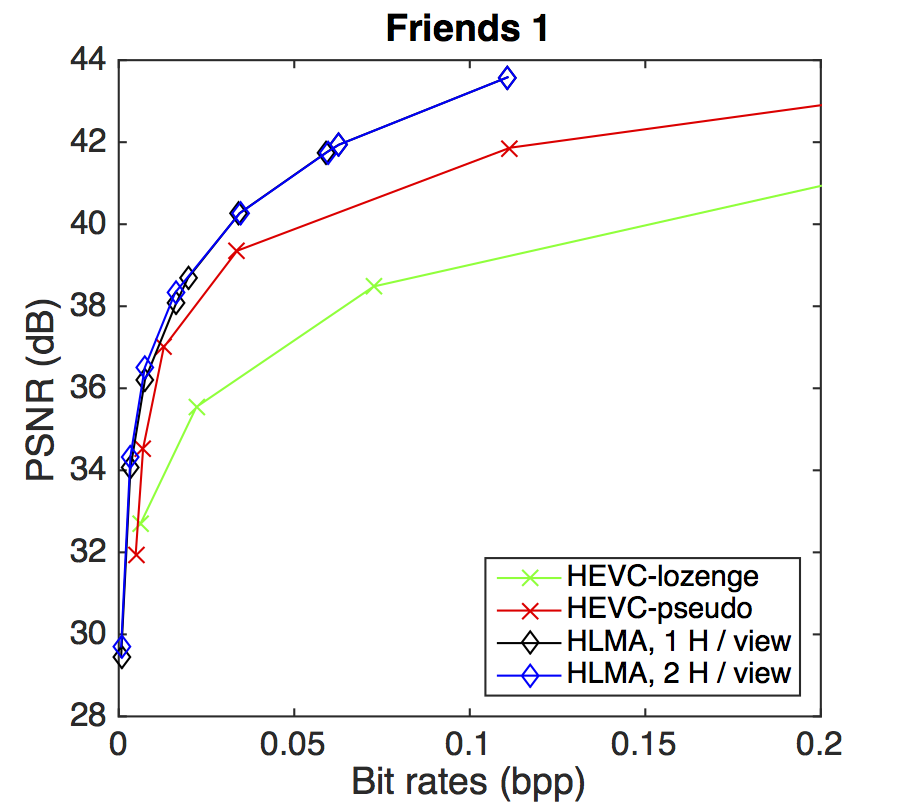
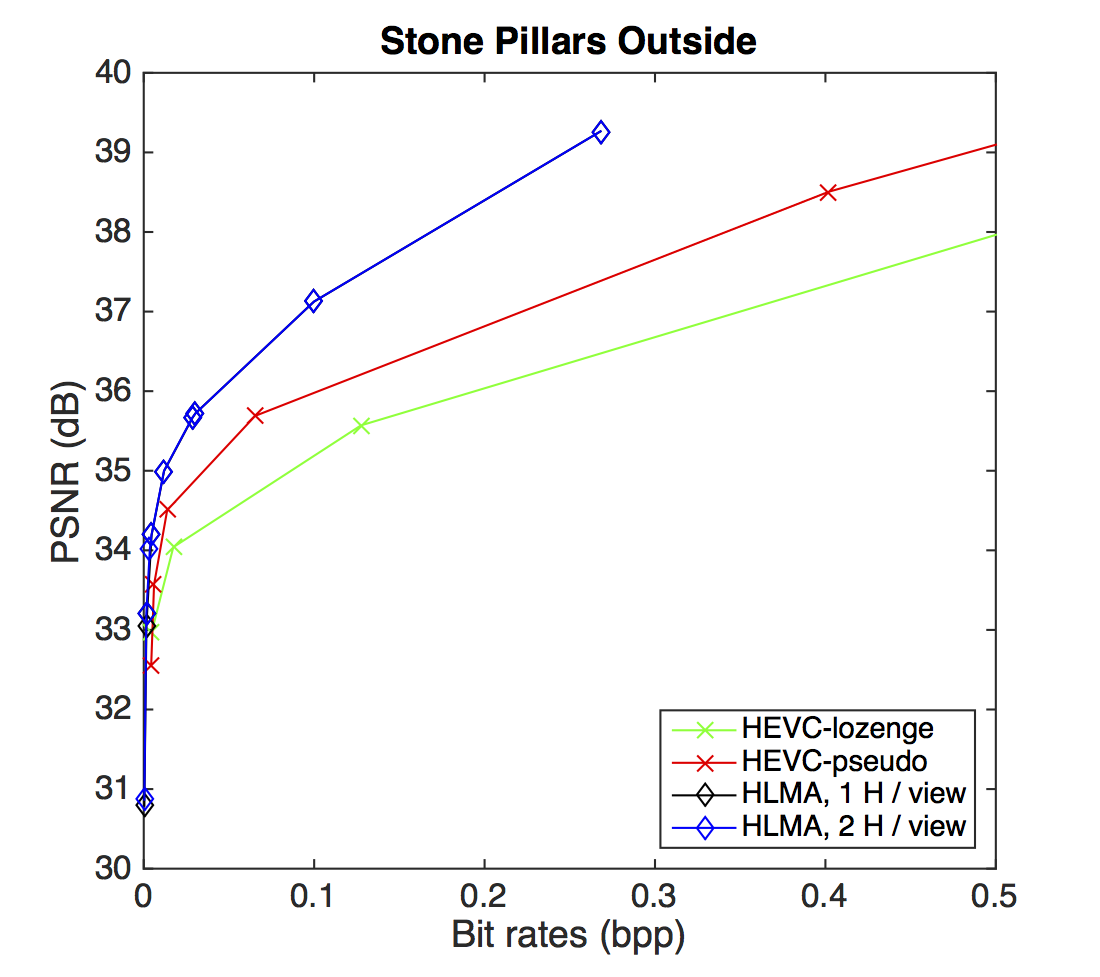
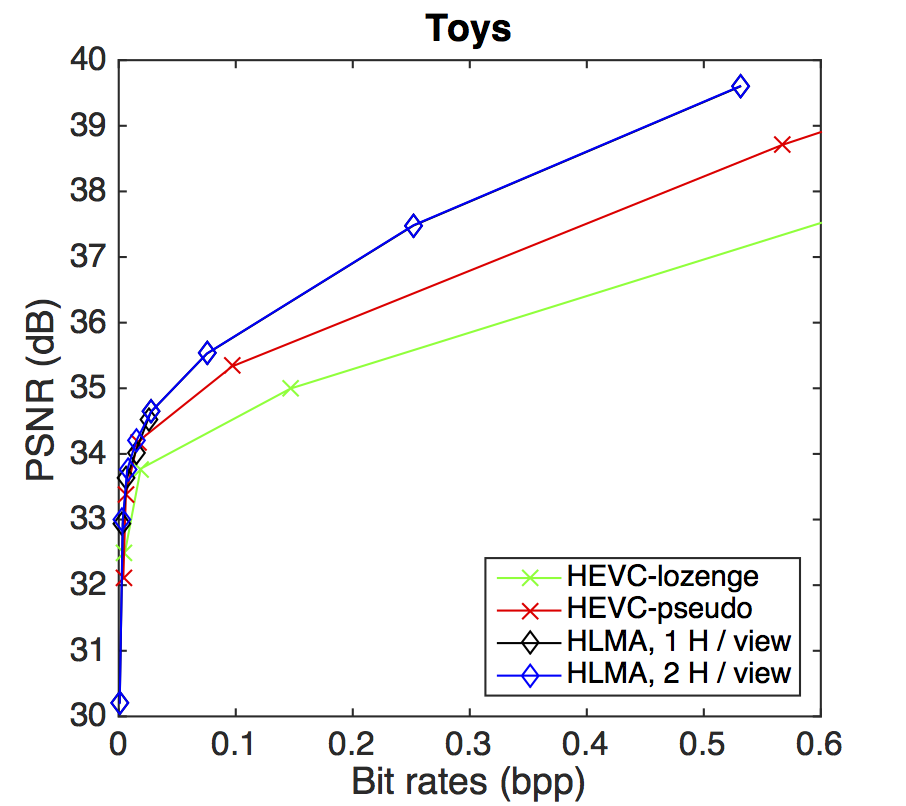
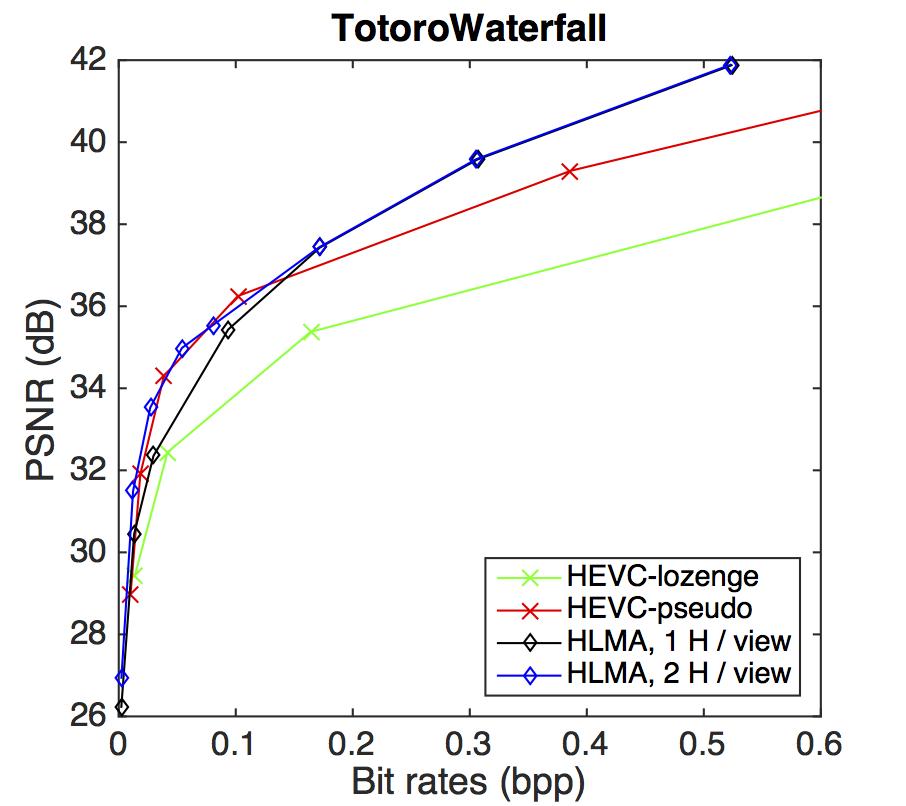
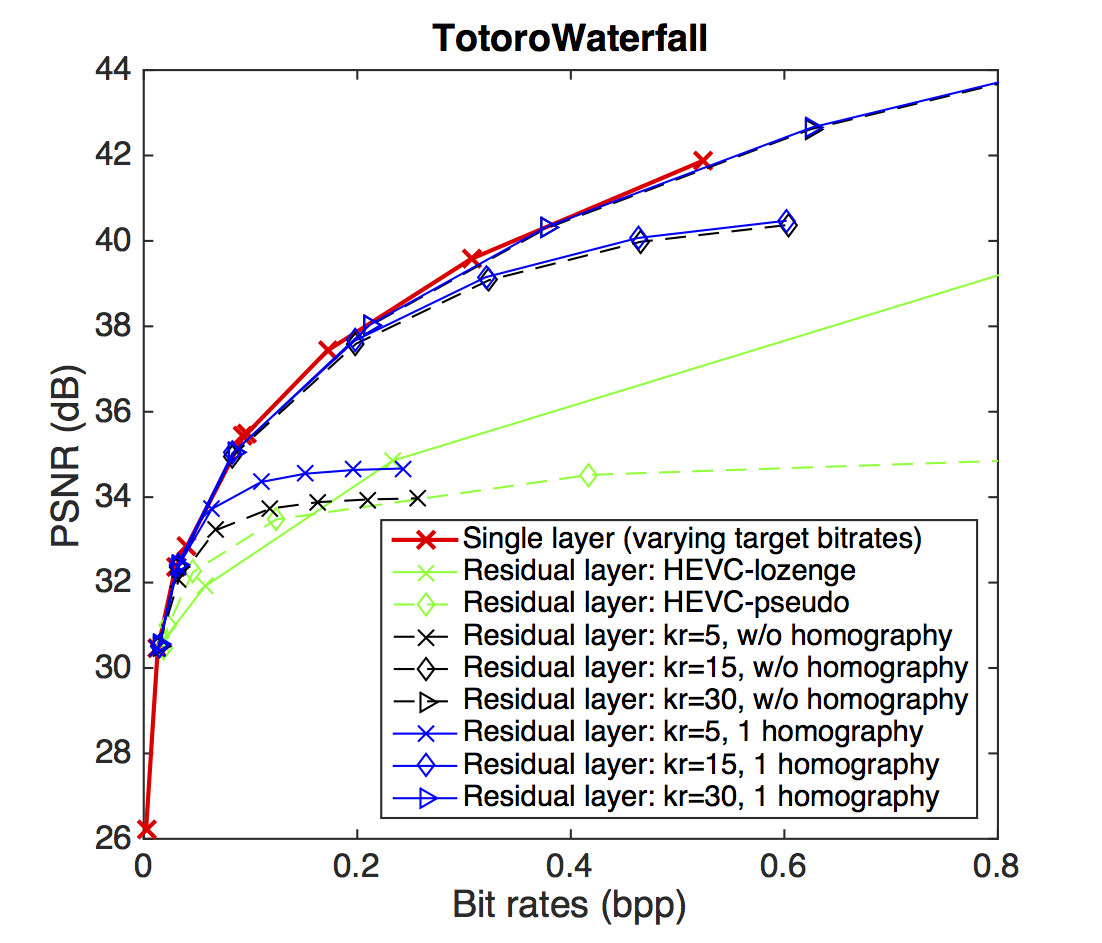
PSNR-rate performance

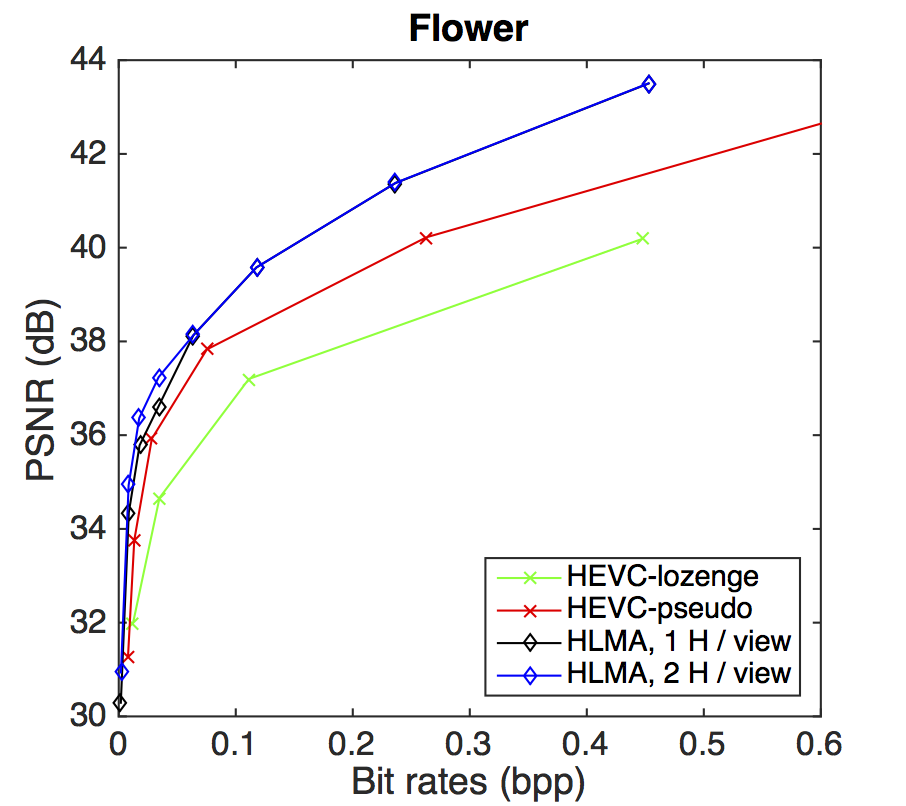We assess the compression performance obtained with the homography-based low rank approximation against two schemes: direct encoding of the views as a pseudo-video sequence according to a lozenge order (HEVC-lozenge) and according to the hierarchical scanning order (HEVC-pseudo).

BD-PSNR gains with respect to HEVC-lozenge scheme. The gains are shown for the HEVC-pseudo and for our HLRA scheme with one or two homographies per view.

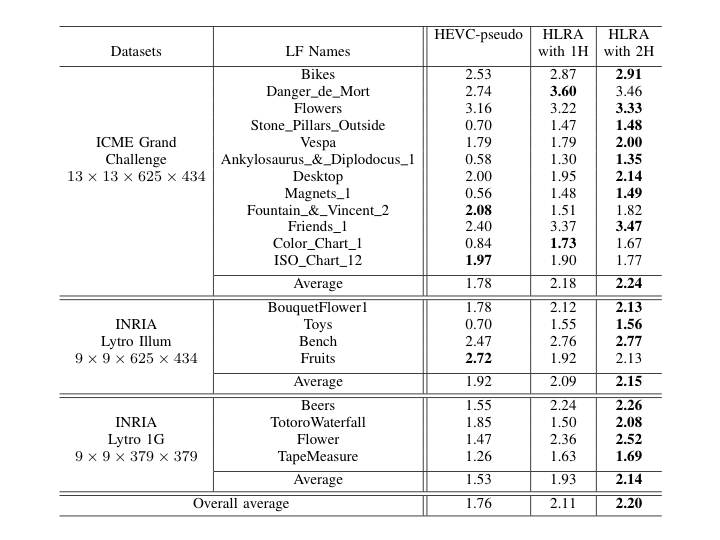Run Times

Complexity comparison. The results are averaged over the test light fields in different dataset. The consumed time is measured at QP=20 both for HLRA and HEVC-pseudo.

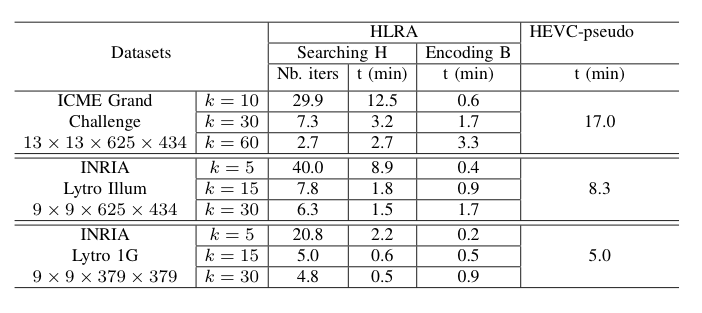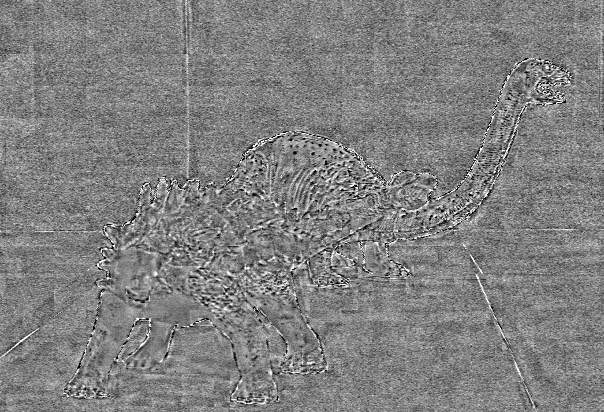
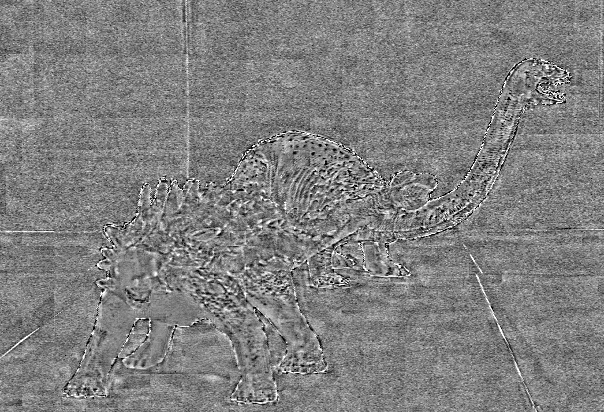
Approximation error

Original center view	HEVC-lozenge	HEVC-pseudo	HLRA

Ankylosaurus Diplodocus 1	PSNR=38.70 dB, bitrate=7.8 × 10^-3 bpp	PSNR=37.92 dB, bitrate=5.2 × 10^-3 bpp	PSNR=39.79 dB, bitrate=3.5 × 10^-3 bpp

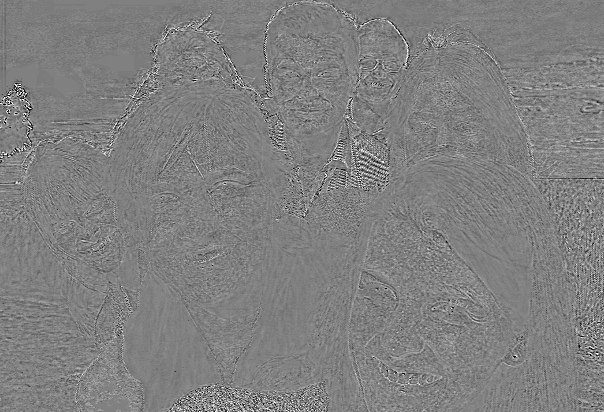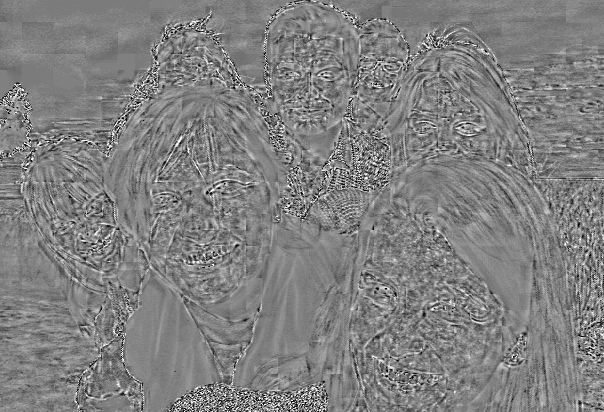
Friends 1	PSNR=32.68 dB, bitrate=6.1 × 10^-3 bpp	PSNR=34.54 dB, bitrate=6.9 × 10^-3 bpp	PSNR=36.50 dB, bitrate=7.4 × 10^-3 bpp

Stone Pillars Outside	PSNR=34.04 dB, bitrate=1.7 × 10^-2 bpp	PSNR=34.54 dB, bitrate=1.5 × 10^-2 bpp	PSNR=36.50 dB, bitrate=1.2 × 10^-2 bpp

Comparison original vs. compressed light fields

TotoroWaterfall

Left: the original light field. Right: the compressed light field with k = 5 and q = 2 (number of depth planes) and HEVC-QP=14. The average PSNR on all views is 35.0 dB and the average bit-rate is 0.05 bpp.

Flower

Left: the original light field. Right: the compressed light field with k = 5 and q = 2 and HEVC-QP=14. The average PSNR on all views is 37.2 dB and the average bit-rate is 0.03 bpp.

Buddha

Left: the original light field. Middle: the compressed light field with k = 15, q = 2 and HEVC-QP=2. The average PSNR on all views is 43.3 dB and the average bit-rate is 0.14 bpp. Right: the compressed light field with k = 15, q = 4 and HEVC-QP=2. The average PSNR on all views is 44.1 dB and the average bit-rate is 0.13 bpp.

Scalable light field coding

We propose a scalable extension of our method where the residual between the original and the decoded light field is encoded as an enhancement layer. The base layer is computed by encoding the original light field with HLRA using a single homography. For the residual layer, four coding schemes are tested: 1-/ HEVC-lozenge; 2-/ HEVC pseudo; 3-/ HLRA without alignment; 4-/ HLRA with one homography. The simulation shows that a simpler coding scheme only based on matrix factorization is sufficient and it substantially outperforms the HEVC inter encoding of the pseudo-sequence of view residuals.