High Dynamic Range Light Fields via Weighted Low Rank Approximation
 |
M. Le Pendu, A. Smolic, C. Guillemot,
"High Dynamic Range Light Fields via Weighted Low Rank Approximation", IEEE Internation Conf. on Image Processing, submitted, 2018.(pdf) Collaboration with Trinity College Dublin |
Abstract
In this paper, we propose a method for capturing High Dynamic
Range (HDR) light fields with dense viewpoint sampling. Analogously
to the traditional HDR acquisition process, several light
fields are captured at varying exposures with a plenoptic camera.
The RAW data is de-multiplexed to retrieve all light field viewpoints
for each exposure and perform a soft detection of saturated
pixels. Considering a matrix which concatenates all the vectorized
views, we formulate the problem of recovering saturated
areas as a Weighted Low Rank Approximation (WLRA) where
the weights are defined from the soft saturation detection. We
show that our algorithm successfully recovers the parallax in the
over-exposed areas while the Truncated Nuclear Norm (TNN)
minimization, traditionally used for single view HDR imaging,
does not generalize to light fields. Advantages of our weighted
approach as well as the simultaneous processing of all the viewpoints
are also demonstrated in our experiments.
Soft Saturation Detection
The plenoptic RAW data is first de-multiplexed into light field views using the toolbox of [1] with the enhancements of [2]. Soft saturation detection is performed directly on sensor data (i.e. before the devignetting and demosaicing steps).
For a pixel of normalized value x, we compute its saturation
\begin{equation}
\begin{aligned}
s(x) = \min((x+(1-\tau))^{12}, 1).
\end{aligned}
\end{equation}
In practice, even if a pixel is not fully saturated (x<1), neighboring pixels associated to the other color components on the bayer pattern may saturate. Hence, the level of full saturation τ is set to 0.9 to account for unreliable colors of high pixel values. Similarly to the color data, the sensor saturation image is de-multiplexed using [1] (without devignetting and demosaicing) to obtain a saturation map of each light field view.
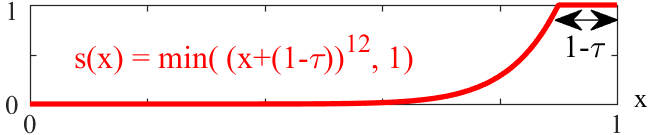 |
Weighted Low Rank Approximation
In order to cope with possible movements of the camera when capturing the different exposures, all the views of the low exposure light fields are aligned to the high exposure one using HLRA [3]. For fast computations, homography parameters are determined only from the central views of the high and low exposure light fields. Prior to WLRA, we convert RGB data to
luminance Y and CIE chromaticity components u'v'. The saturation s is converted into weights w as:
\begin{equation}
\begin{aligned}
w=\frac{1-s}{s+1/w_{max}}.
\end{aligned}
\end{equation}
The non-saturated pixels (s = 0) are thus associated to the maximum
weight indicating a high confidence, while the fully
saturated pixels (s = 1) have a null weight. In our experiments,
we use wmax = 100.
Finally, weights and image data are arranged into respective
matrices, each column contains a
vectorized light field view.
Our WLRA method generalizes the matrix completion algorithm in [4] to the case of non-binary weights. Given the matrix M to approximate, a global noise tolerance parameter ε, and the element-wise weight matrix W, the problem formulation is: \begin{equation} \begin{aligned} \min_{X} &\quad \mathrm{rank}(X)\\[-2pt] \text{s.t.} &\quad X=Z\\[-3pt] &\quad ||{W\circ(Z-M)}||_F^2\leq\epsilon, \end{aligned} \label{eq:WLRAeq} \end{equation} where the operator "o" is the element-wise multiplication. The introduction of the matrix Z and the constraint X=Z makes it possible to use the Alternating Direction Method of Multipliers. For more details on the way the problem is solved, please refer to our paper.
Our WLRA method generalizes the matrix completion algorithm in [4] to the case of non-binary weights. Given the matrix M to approximate, a global noise tolerance parameter ε, and the element-wise weight matrix W, the problem formulation is: \begin{equation} \begin{aligned} \min_{X} &\quad \mathrm{rank}(X)\\[-2pt] \text{s.t.} &\quad X=Z\\[-3pt] &\quad ||{W\circ(Z-M)}||_F^2\leq\epsilon, \end{aligned} \label{eq:WLRAeq} \end{equation} where the operator "o" is the element-wise multiplication. The introduction of the matrix Z and the constraint X=Z makes it possible to use the Alternating Direction Method of Multipliers. For more details on the way the problem is solved, please refer to our paper.
Experimental Results
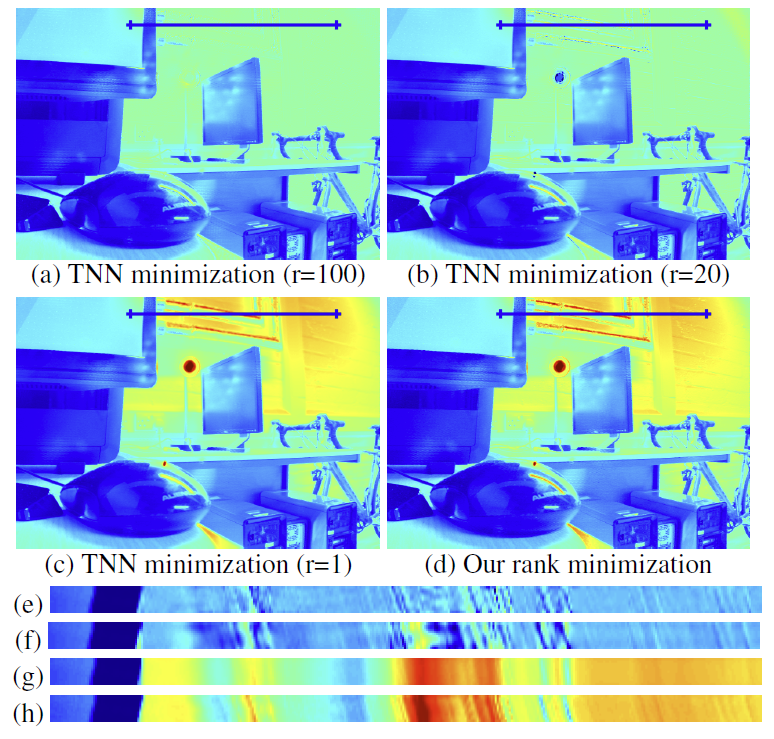
Evaluation of the Rank Minimization compared with the Truncated Nuclear Norm Minimization
In single view HDR imaging, existing low rank based methods
minimize the Truncated Nuclear Norm (TNN) with r = 1 as the matrix rank can
be assumed to be 1. However, this assumption does not hold
for light fields with disparities between views, and produces blur
in the completed regions as shown in Figures (c),(g) below. Using higher
values of r keeps the details but not the low spatial frequencies
(Figures (a),(b),(e),(f)). Our rank minimization successfully recovers
both low and high frequencies (Figures (d),(h)).
The figure below shows: (a)-(d) show the central view in false color for each method of a 13x13 HDR Light field reconstructed from 3 exposures. (e),(f),(g),(h) are the epipolar images corresponding to the blue segment in (a),(b),(c),(d) respectively (vertical axis shows vertical viewpoint change). The epipolar image in (g) shows that the structures completed using TNN minimization with r=1 are blurred and identical in all the views (parallax is not preserved).
The figure below shows: (a)-(d) show the central view in false color for each method of a 13x13 HDR Light field reconstructed from 3 exposures. (e),(f),(g),(h) are the epipolar images corresponding to the blue segment in (a),(b),(c),(d) respectively (vertical axis shows vertical viewpoint change). The epipolar image in (g) shows that the structures completed using TNN minimization with r=1 are blurred and identical in all the views (parallax is not preserved).
 |
Recovery of saturated areas from two exposures
One view of a HDR light field captured from two significantly different exposures (images are gamma encoded for display purpose). Some over-exposed areas in the high exposure capture are under-exposed in the low exposure one. Independent processing of the viewpoints (a) highlights the presence of noise due to underexposition. Using all the viewpoints in the WLRA (b) naturally exploits redundancies to reduce the noise.Video of (left) original light field, (right) HDR reconstructed light field represented in false colors to show the coherency between the views.

To play the video click on the image |
|---|
Video showing the sub-apertures with a progressive change of exposure.

To play the video click on the image |
|---|
References
- D. G. Dansereau, O. Pizarro, and S. B. Williams, Decoding, calibration and rectification for lenselet-based plenoptic cameras,in Proc. CVPR, 2013, pp. 1027–1034.
- P. David, M. Le Pendu, and C. Guillemot, White lenslet image guided demosaicing for plenoptic cameras, in IEEE 19th International Workshop on Multimedia Signal Processing (MMSP), Oct. 2017, pp.1-6.
- X. Jiang, M. Le Pendu, R. A. Farrugia, and C. Guillemot, Light field compression with homography-based low-rank approximation, IEEE Journal of Selected Topics in Signal Processing, vol. 11, no. 7, pp. 1132-1145, Oct. 2017.
- M. Le Pendu, X. Jiang, and C. Guillemot, Light field inpainting propagation via low rank matrix completion, IEEE Transactions on Image Processing, vol. 27, no. 4, pp.1981-1993, Apr. 2018