Prediction and Sampling with Local Graph Transforms for Quasi-Lossless Light Field Compression
 |
M. Rizkallah, T. Maugey and C. Guillemot,
"Prediction and Sampling with Local Graph Transforms for Quasi-Lossless Light Field Compression", IEEE Transactions on image processing, Dec. 2019.(pdf) |
Abstract
Graph-based transforms have been shown to be powerful tools in terms of image energy compaction. However, when the size of the support increases to best capture signal dependencies, the computation of the basis functions becomes rapidly untractable. This problem is in particular compelling for high dimensional imaging data such as light fields. The use of local transforms with limited supports is a way to cope with this
computational difficulty. Unfortunately, the locality of the support may not allow us to fully exploit long term signal dependencies present in both the spatial and angular dimensions of light fields. This paper describes sampling and prediction schemes with local graph-based transforms enabling to efficiently compact the signal energy and exploit dependencies beyond the local graph support. The proposed approach is investigated and is shown to be very efficient in the context of spatio-angular transforms for quasi-lossless compression of light fields.
Super-ray based Local Graph Transforms
Geometry-aware Local Supports: general method
The method proposed to define the local supports consists of the following steps
- Compute the segmentation of the top-left view
- Estimate the disparity map of the top-left view from the light field
- Using the median disparity per super-pixel to project the labels from the top-left to the other views
- Appearing pixels are grouped with the neighboring background super-ray
- Occluded pixels are grouped with the neighboring foreground super-ray
 |
 |
| Fountain Vincent | Flower 2 |
Local graph transforms
In order to jointly capture spatial and angular correlations between pixels in the light field, we first consider a local non separable graph per super-ray.
More precisely, if we consider the luminance values in the whole light field and a segmentation map S, the super-ray K can be represented by
a signal defined on an undirected connected graph G = {V,E} which consists of a finite set V of vertices.
A set E of edges are built as follows.
The laplacian is computed as:
The non separable graph transform is defined as the projection of the graph signal onto the eigenvectors of the laplacian.
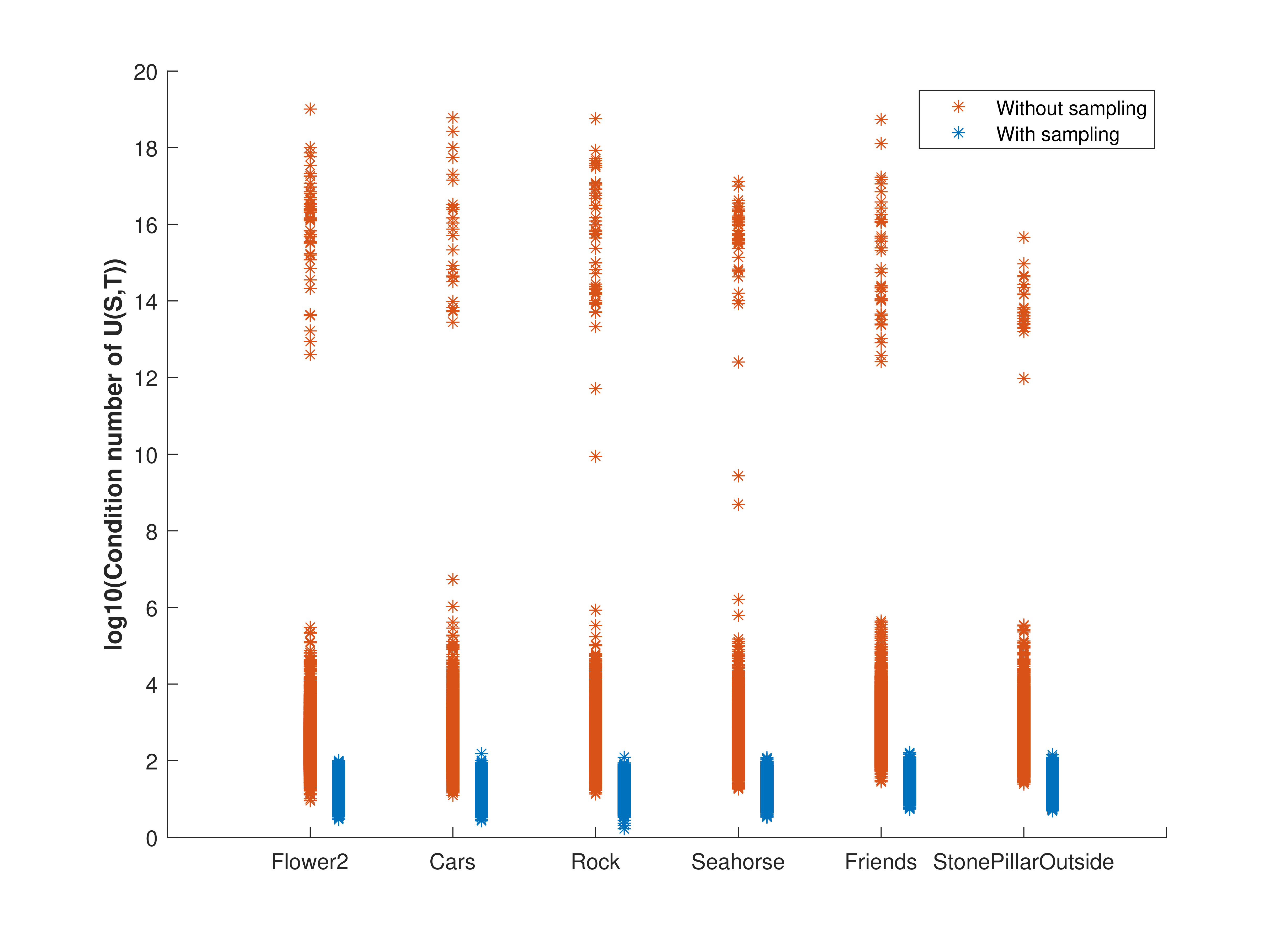
However, some high complexity remains. That's why we propose to use instead separable graph transforms where we perform a spatial transform followed by an angular transform. The spatial laplacian is defined in each view. Using the eigenvectors of the spatial laplacian, we can compute a spatial transform inside each view. We can then define a band vector out of all observations of a specific band across the views and construct an angular graph to capture inter-view correlations. Using the eigenvectors of the angular laplacian, we compute the second angular transform.
- We first connect each pixel (m,n,x,y) in the set V and its 4-nearest neighbors in the spatial domain (i.e. the top, bottom, left and right neighbors)
- We then find the median disparity value d of the pixels inside the super-ray k in the top-left view. Using this disparity value, we project each pixel in super-ray k in the 4 nearest neighboring views (i.e. the top, bottom, left and right neighboring view). We end up with four projected pixels. If a projected pixel belongs to the set of vertices V, then we connect it to the original pixel.
The laplacian is computed as:
The non separable graph transform is defined as the projection of the graph signal onto the eigenvectors of the laplacian.
However, some high complexity remains. That's why we propose to use instead separable graph transforms where we perform a spatial transform followed by an angular transform. The spatial laplacian is defined in each view. Using the eigenvectors of the spatial laplacian, we can compute a spatial transform inside each view. We can then define a band vector out of all observations of a specific band across the views and construct an angular graph to capture inter-view correlations. Using the eigenvectors of the angular laplacian, we compute the second angular transform.
Super-ray based Graph Prediction and Sampling
The prediction and sampling scheme with a local graph transform applied on a super-ray consists of the following:
- On the encoder side, we find the best set of reference samples.
- A local graph transform is applied.
- The reference samples (surrounded in yellow) are projected in a reference image (as shown with the blue arrows).
- The high frequencies and the reference image are both sent to the decoder.
- The decoder predicts the low frequency transform coefficients then recovers the original super-ray by inverse local graph transform.
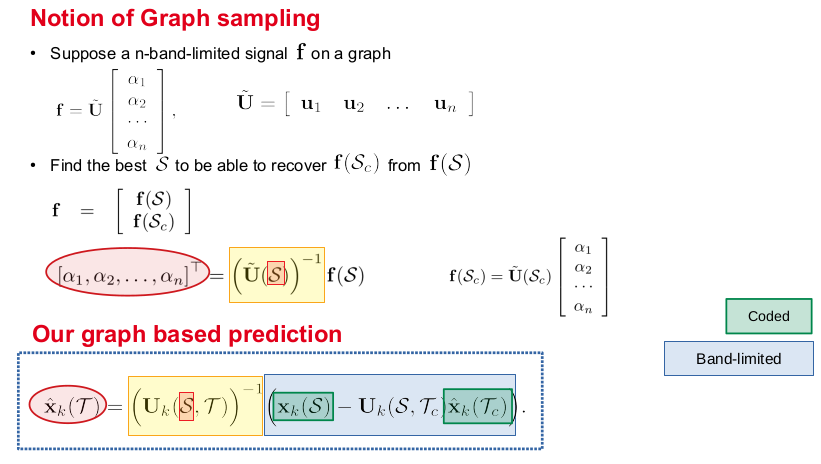
How to perform a Graph based Prediction ?
How to choose the samples ?
Proposed coding schemes based on local graph based transforms
Proposed coding scheme with the non separable graph transform
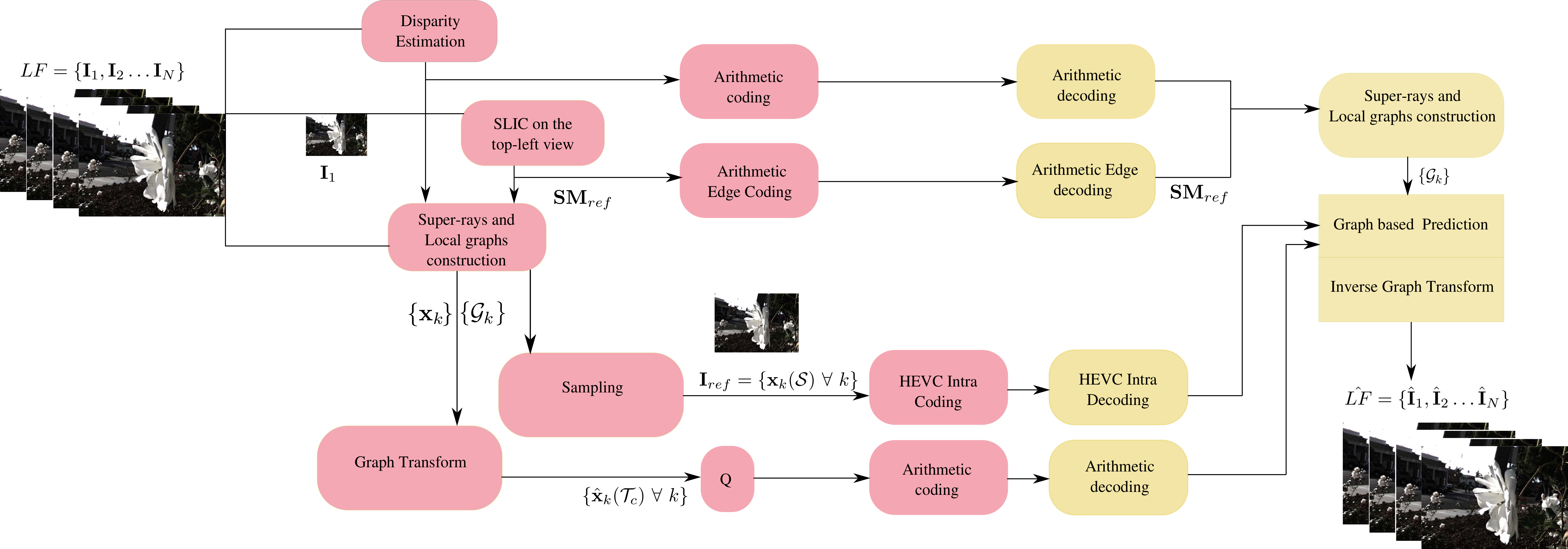
The coding scheme with a local non separable graph transform consists of the following: The encoder sends:
- a segmentation map of the top-left view using the arithmetic edge coder
- a sparse set of disparity values using arithmetic coding.
- a reference image consisting of the set of samples coded with HEVC
- the high frequency coefficients of all super-rays after applying the non separable graph fourier transform with adaptive CABAC coding
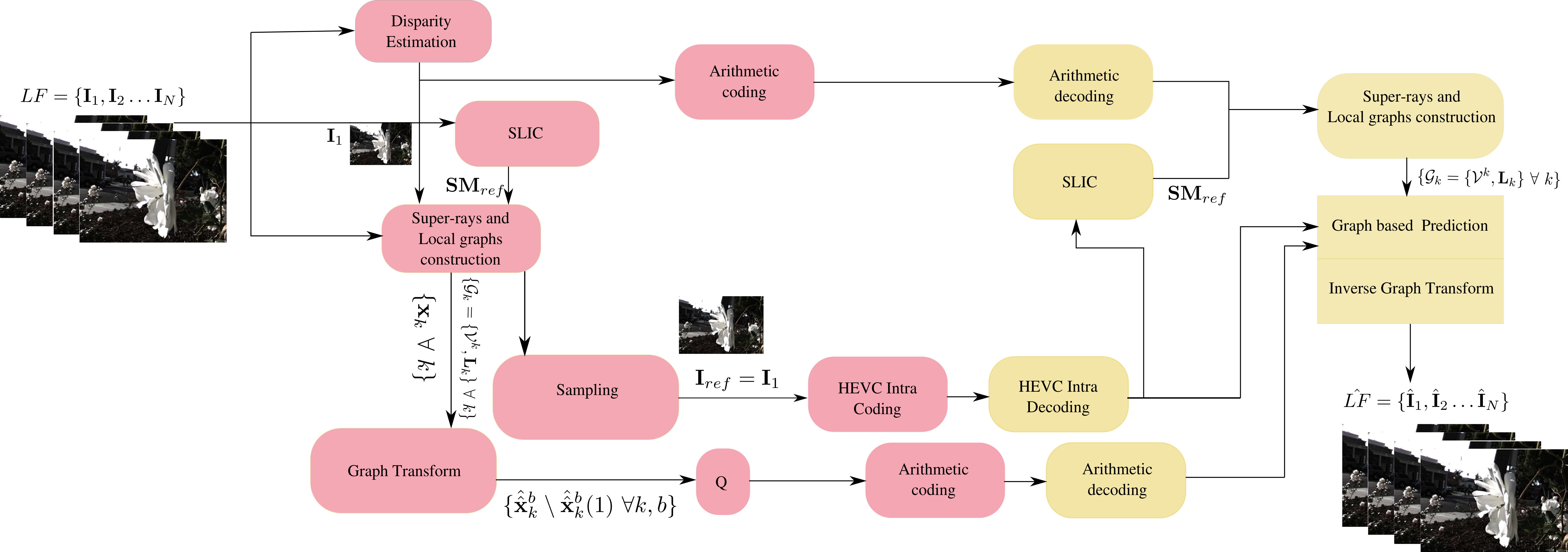
Proposed coding scheme with the separable graph transform
Experimental results
Energy compaction
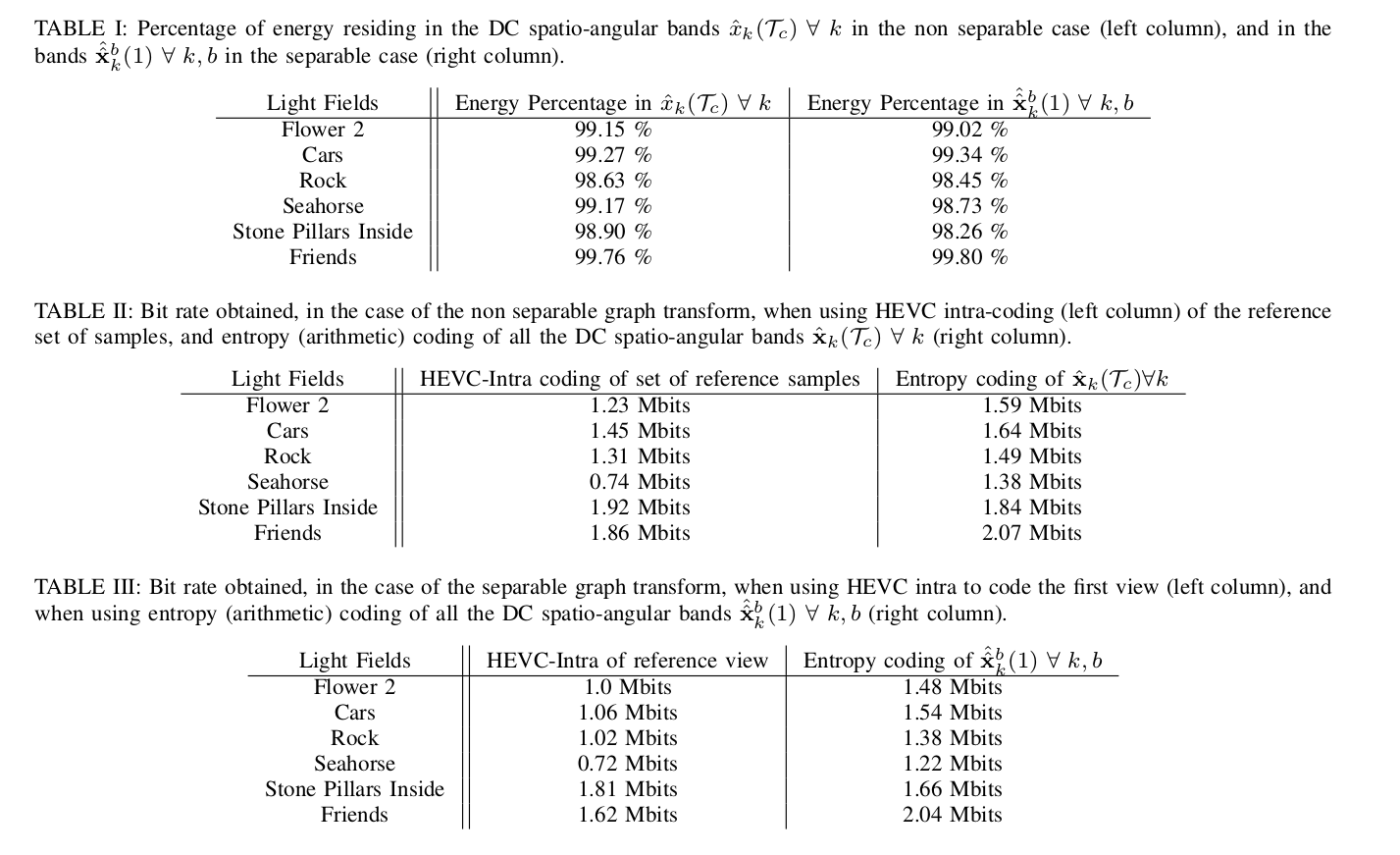
Efficiency of the prediction
Performance comparison against state of the art coders
- Around 30 % gain in bit rate with respect to coding the light field as a video sequence with HEVC inter for high PSNR
- Non separable graph transform more sensitive to quantization errors

