Geometry-aware graph Transforms for Light Field Compact representations
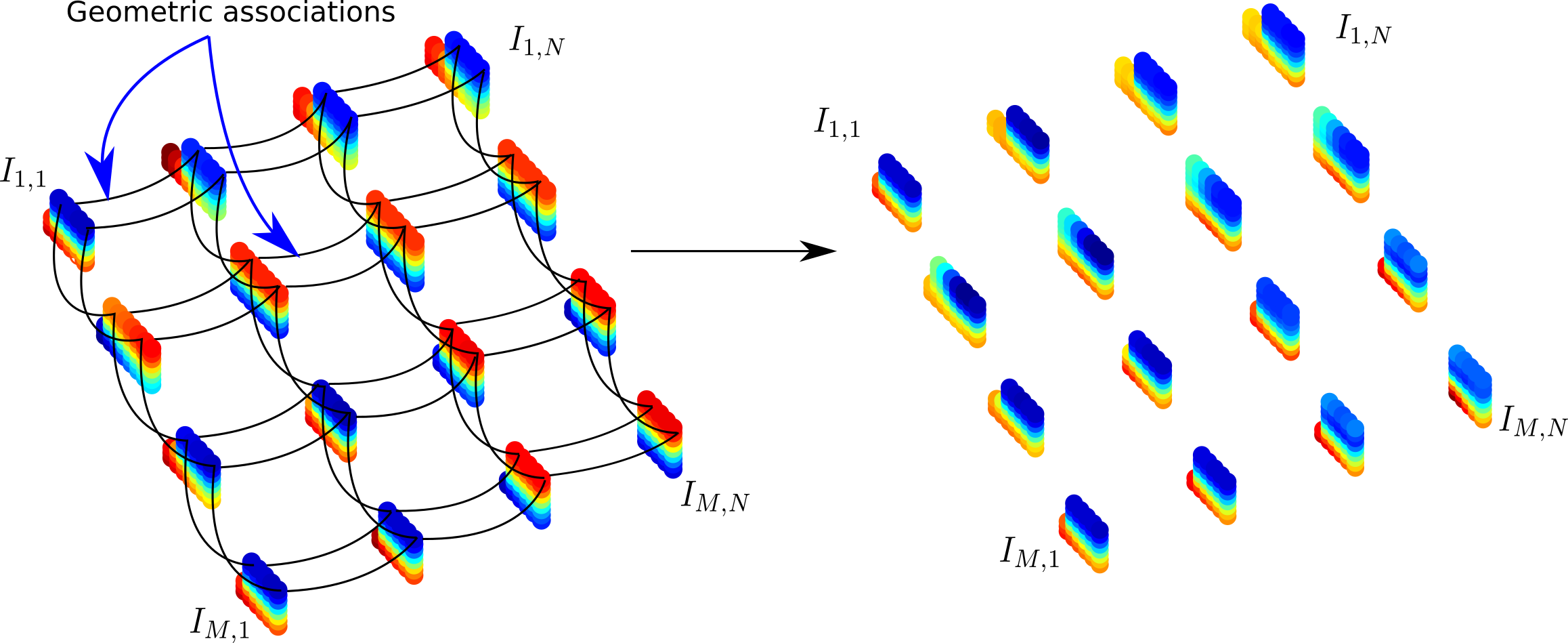 |
M. Rizkallah, X. Su, T. Maugey and C. Guillemot,
"Geometry-Aware Graph Transforms for Light Field Compact Representation", to appear in TIP, Aug. 2019.(pdf) |
Abstract
The paper addresses the problem of energy compaction of dense 4D light fields by designing geometry-aware local graph-based transforms. Local graphs are constructed on super-rays that can
be seen as a grouping of spatially and geometry-dependent angularly correlated pixels. Both non separable and separable transforms are considered. Despite the local support of limited size
defined by the super-rays, the Laplacian matrix of the non separable graph remains of high dimension and its diagonalization to compute the transform eigen vectors
remains computa-tionally expensive. To solve this problem, we then perform the local spatio-angular transform in a separable manner. We show that when the shape of corresponding
super-pixels in the different views is not isometric, the basis functions of the spatial transforms are not coherent, resulting in decreased correlation between spatial transform coefficients.
We hence propose anovel transform optimization method that aims at preserving angular correlation even when the shapes of the super-pixels are not isometric. Experimental results
show the benefit of the approach in terms of energy compaction. A coding scheme is also described to assess the rate-distortion perfomances of the proposed transforms and is compared to state
of the art encoders namely HEVC and JPEG Pleno VM 1.1.
Geometry-aware Local Supports for Light Fields
Geometry-aware local supports: general method
The method proposed to define the local supports consists of the following steps
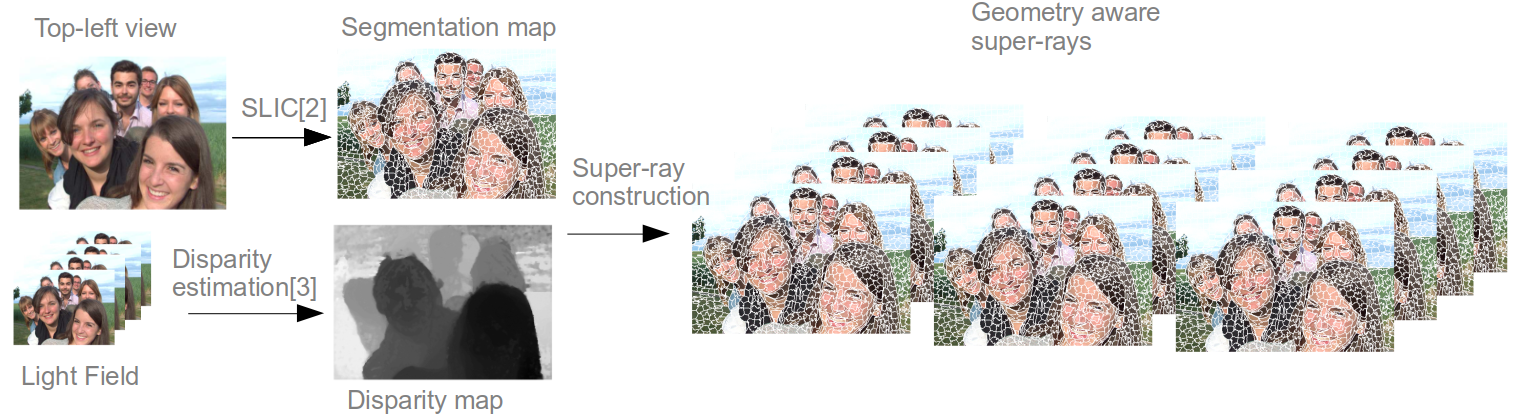
- Compute the segmentation of the top-left view
- Estimate the disparity map of the top-left view from the light field
- Using the median disparity per super-pixel to project the labels from the top-left to the other views
- Appearing pixels are grouped with the neighboring background super-ray
- Occluded pixels are grouped with the neighboring foreground super-ray


Results on Light Fields data
In this section, we assess how the proposed super-ray construction method deals with occluded and dis-occluded parts, and to which extent the super-rays are consistent despite uncertainty
on the disparity information. The following figure shows examples of super-rays obtained with different synthetic light fields ( butterfly and Monasroom) and real light fields captured by
a Lytro Ilum camera (Flower 2, Rock, FountainVincent and StonePillarInside).In the first three columns, we have the original top left corner view, its corresponding disparity map and super
pixel segmentation using the SLIC algorithm [ref] respectively. In the fourth column, we show horizontal and vertical epipolar segments taken both from the 4D light field color information
and our final segmentation in specific regions of the image (the red blocks). We can see that we are following well the object borders, especially when the disparity map is reliable. Also
, we have always attained a high percentage of coherent super-rays across views (higher than $40\%$ as measured with Cons(%) in the fifth column). More precisely, Cons(%) gives the
percentage of coherent super-rays: A super-ray is coherent when it is made of super pixels having the same shape in all the views, with or without a displacement.

The non separable graph transform is defined as the projection of the graph signal onto the eigenvectors of the laplacian.
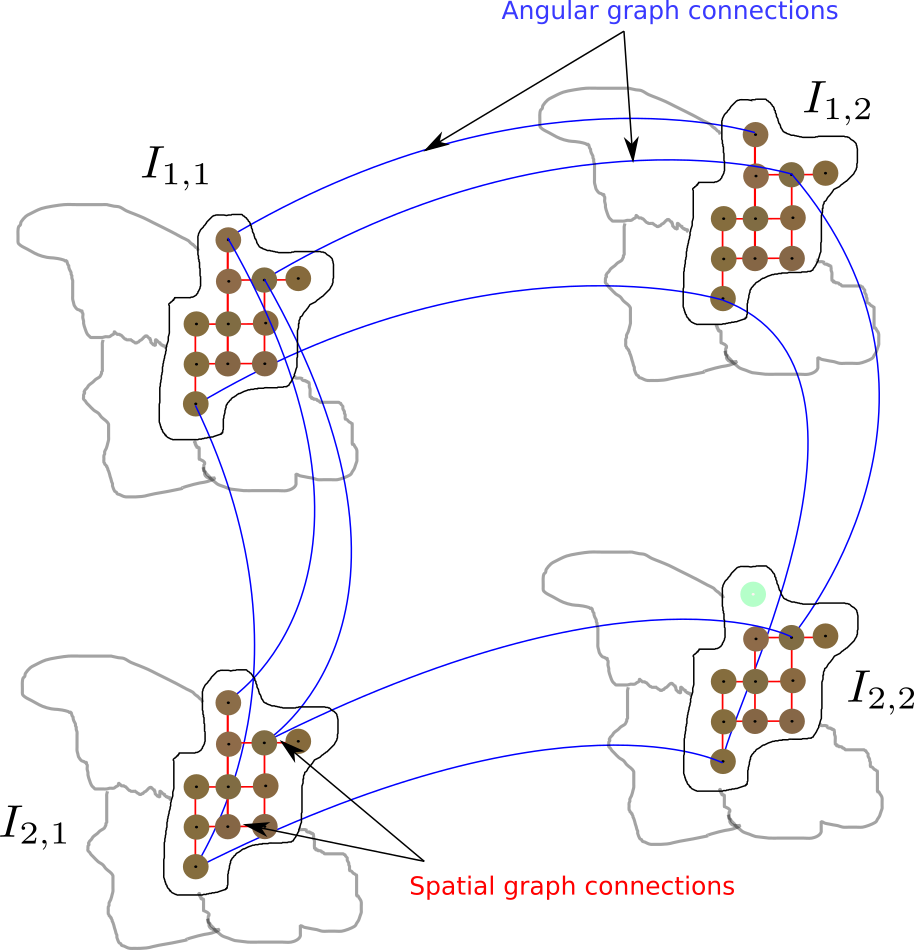
However, some high complexity remains. That's why we propose to use instead separable graph transforms where we perform a spatial transform followed by an angular transform.
The spatial laplacian is defined in each view. Using the eigenvectors of the spatial laplacian, we can compute a spatial transform inside each view.
We can then define a band vector out of all observations of a specific band across the views and construct an angular graph to capture inter-view correlations.
Using the eigenvectors of the angular laplacian, we compute the second angular transform.
For the shape varying super-rays, we end up with incompatible basis functions that will no longer preserve the angular correlations.
We propose in this paper an optimization that is able to make the spatial basis functions coherent accross the views. The optimization problem is defined between two views: the reference view and a target view for a specific super-ray as the following

An example of a result of the optimization on one eigenvector. We show on the left the original eigenvector across the views, on the right the optimized ones. In blue the geometrical connections found
using the estimated disparity.


Animated segmentation maps
| Fountain Vincent | Flower 2 |
 |
 |
Local Graph Transforms
Local graph construction
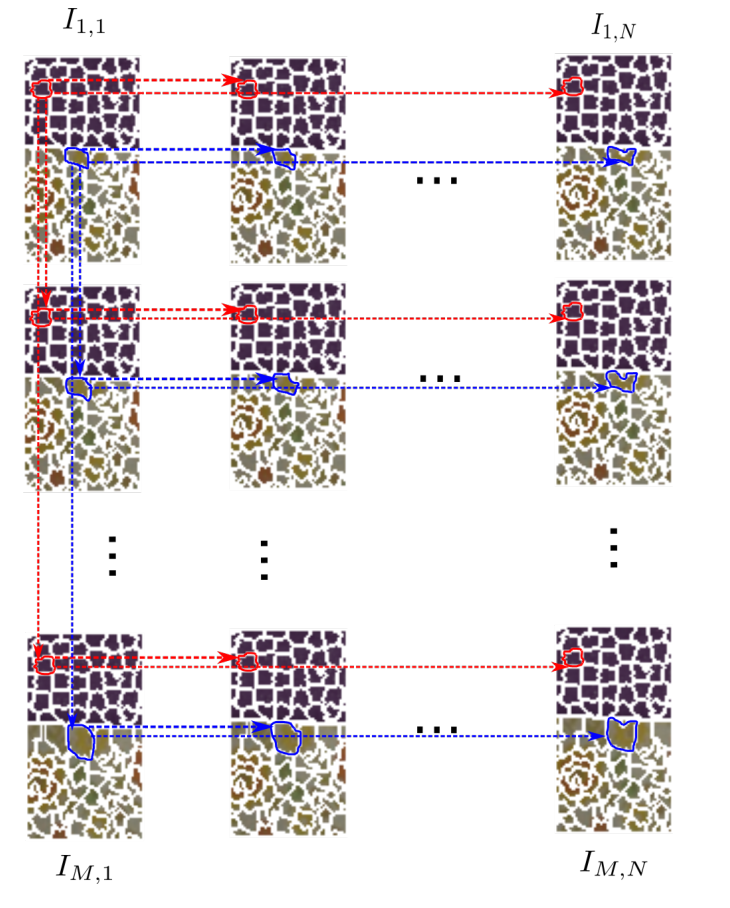
In order to jointly capture spatial and angular correlations between pixels in the light field, we first consider a local non separable graph per super-ray. More precisely, if we consider the luminance values in the whole light field and a segmentation map S, the super-ray K can be represented by a signal defined on an undirected connected graph G = {V,E} which consists of a finite set V of vertices. A set E of edges are built as follows.- We first connect each pixel (m,n,x,y) in the set V and its 4-nearest neighbors in the spatial domain (i.e. the top, bottom, left and right neighbors)
- We then find the median disparity value d of the pixels inside the super-ray k in the top-left view. Using this disparity value, we project each pixel in super-ray k in the 4 nearest neighboring views (i.e. the top, bottom, left and right neighboring view). We end up with four projected pixels. If a projected pixel belongs to the set of vertices V, then we connect it to the original pixel.

Local Non Separable and Separable graph transform
The laplacian is computed as:

Local Optimized Separable Graph Transform
We propose in this paper an optimization that is able to make the spatial basis functions coherent accross the views. The optimization problem is defined between two views: the reference view and a target view for a specific super-ray as the following

Evaluation of the proposed method with real light fields

Some visual results on the EPFL dataset
| Fountain Vincent 2-HEVC Lozenge R=0.1365bpp PSNR=37.18dB | Fountain Vincent 2-JPEG Pleno R=0.1198bpp PSNR=36.29dB | Fountain Vincent 2-Our method(SO) R=0.1976bpp PSNR=39.01dB |
 |
 |
 |
| Friends 1-HEVC Lozenge R=0.1319bpp PSNR=39.5dB | Friends 1-JPEG Pleno R=0.1182bpp PSNR=38.8dB | Friends 1-Our method(SO) R=0.1464bpp PSNR=41.73dB |
 |
 |
 |