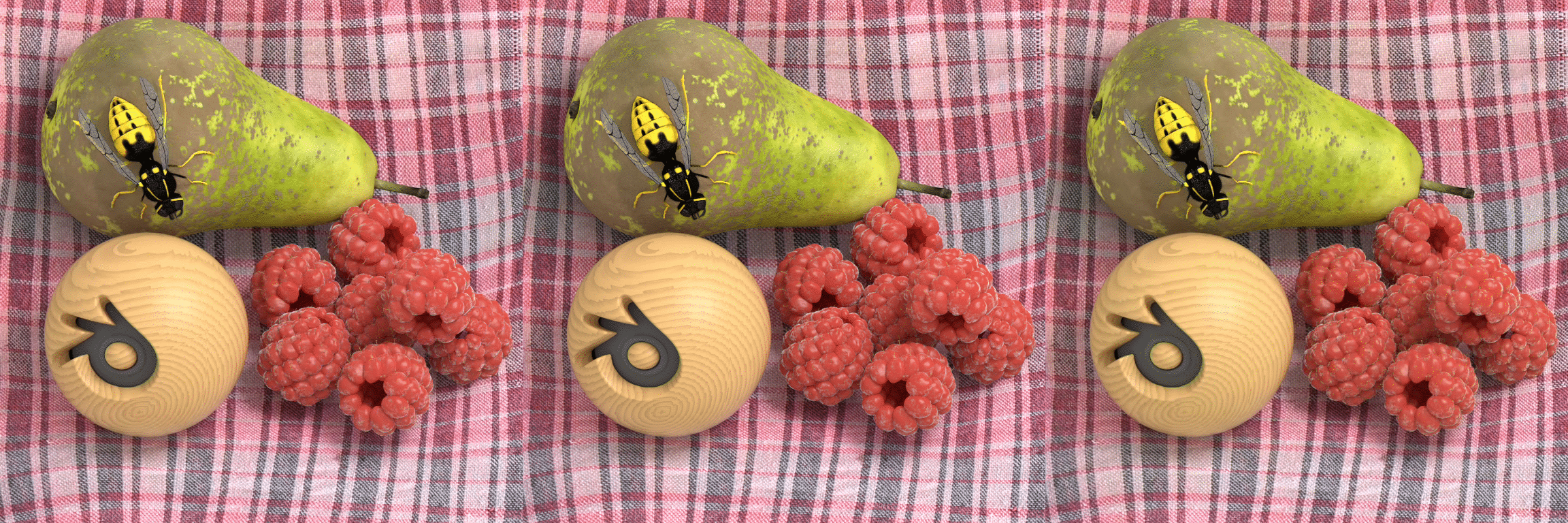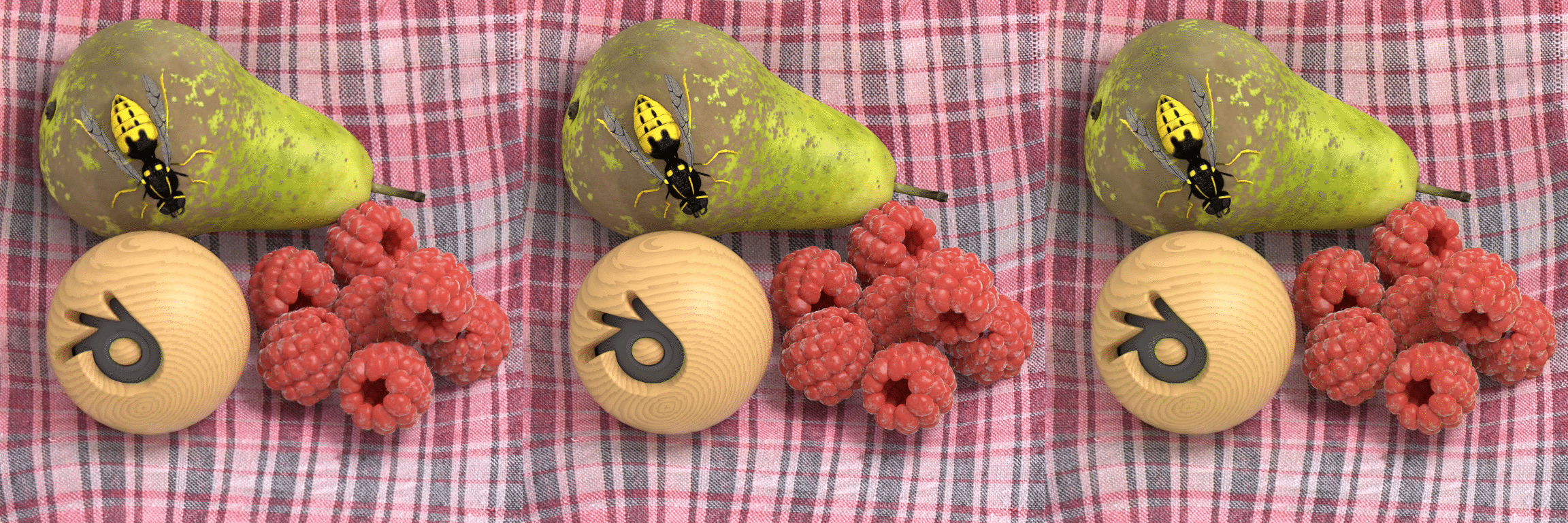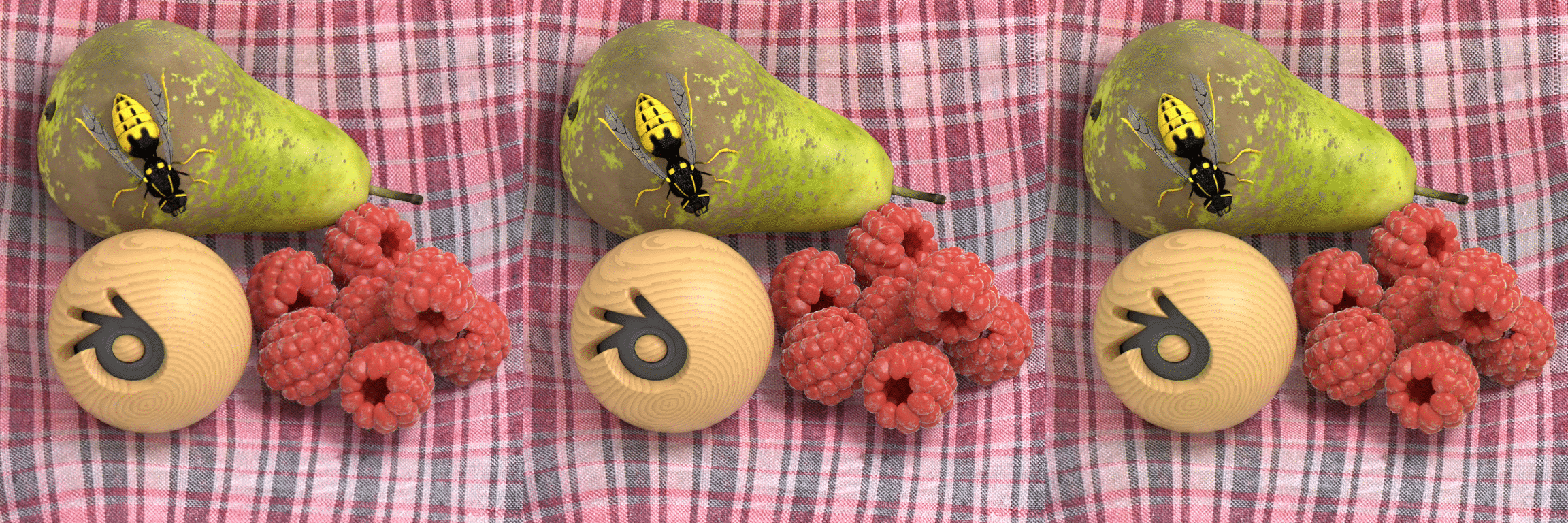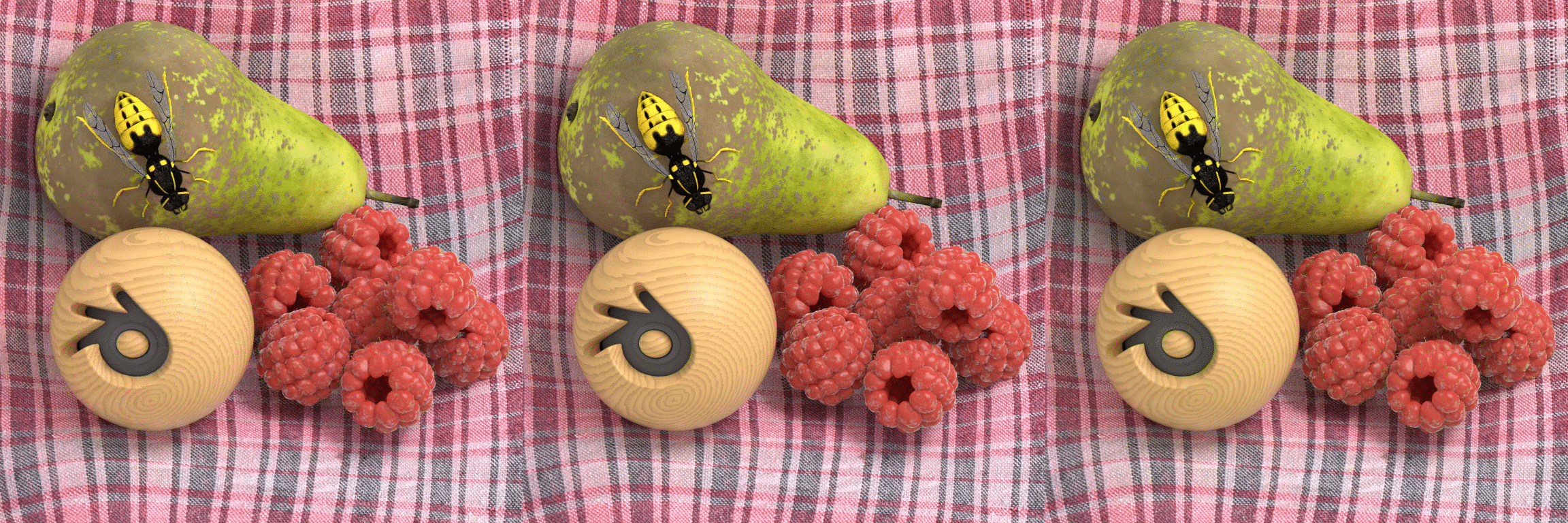Graph-based light fields representation and coding using geometry information
 


 X. Su, M. Rizkallah, T. Maugey, C. Guillemot,

"Graph-based light fields representation and coding using geometry information", IEEE International Conference on Image Processing (ICIP), Beijing, 17-20 Sept. 2017.(pdf)

Abstract

This paper describes a graph-based coding scheme for light fields (LF). It first adapts graph-based representations (GBR) to describe color and geometry information of LF. Graph connections describing scene geometry capture inter-view dependencies. They are used as the support of a weighted Graph Fourier Transform (wGFT) to encode disoccluded pixels. The quality of the LF reconstructed from the graph is enhanced by adding extra color information to the representation for a sub-set of sub-aperture images. Experiments show that the proposed scheme yields rate-distortion gains compared with HEVC based compression (directly compressing the LF as a video sequence by HEVC).

Data sets

We test our GBR on the HCI synthetic LF dataset (9x9 views of 768x768 pixels): Buddha, butterfly, StillLife and monasRoom.




Graph-based representation

Let us denote the graph by G={V,E}, where vertices V correspond to each pixel in sub-aperture images and edges E connect pairs of pixels across two images. As shown in Fig. 1.(a), image I1,1 (left bottom corner image marked in red) is selected as the reference view. Pixels on each row of I1,1 are grouped into a set of straight horizontal segments based on their depth. One segment has a constant depth. As shown in Fig. 1.(b), one row in I1,1 has been divided into 3 segments. Every segment in I1,1 is connected to one segment in every sub-aperture image by one graph edge, since the two segments correspond to the same straight segment in the real 3D world.

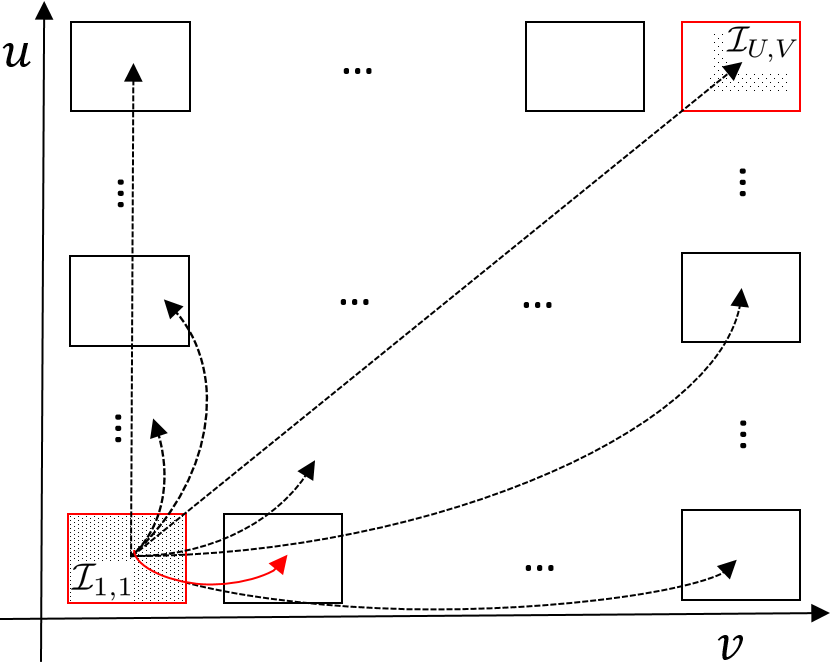
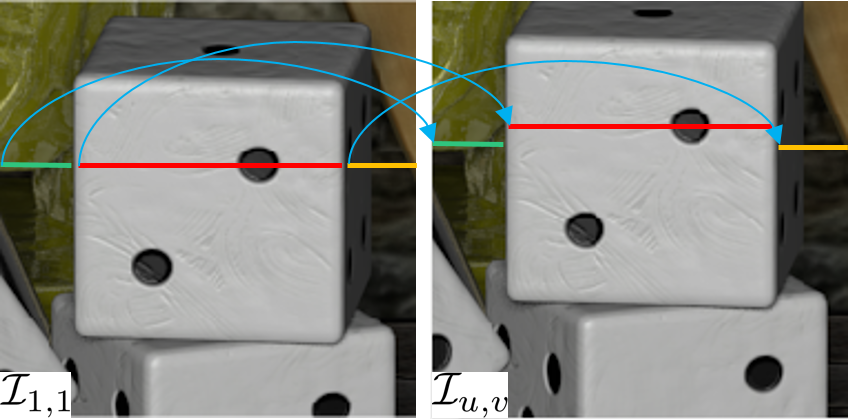
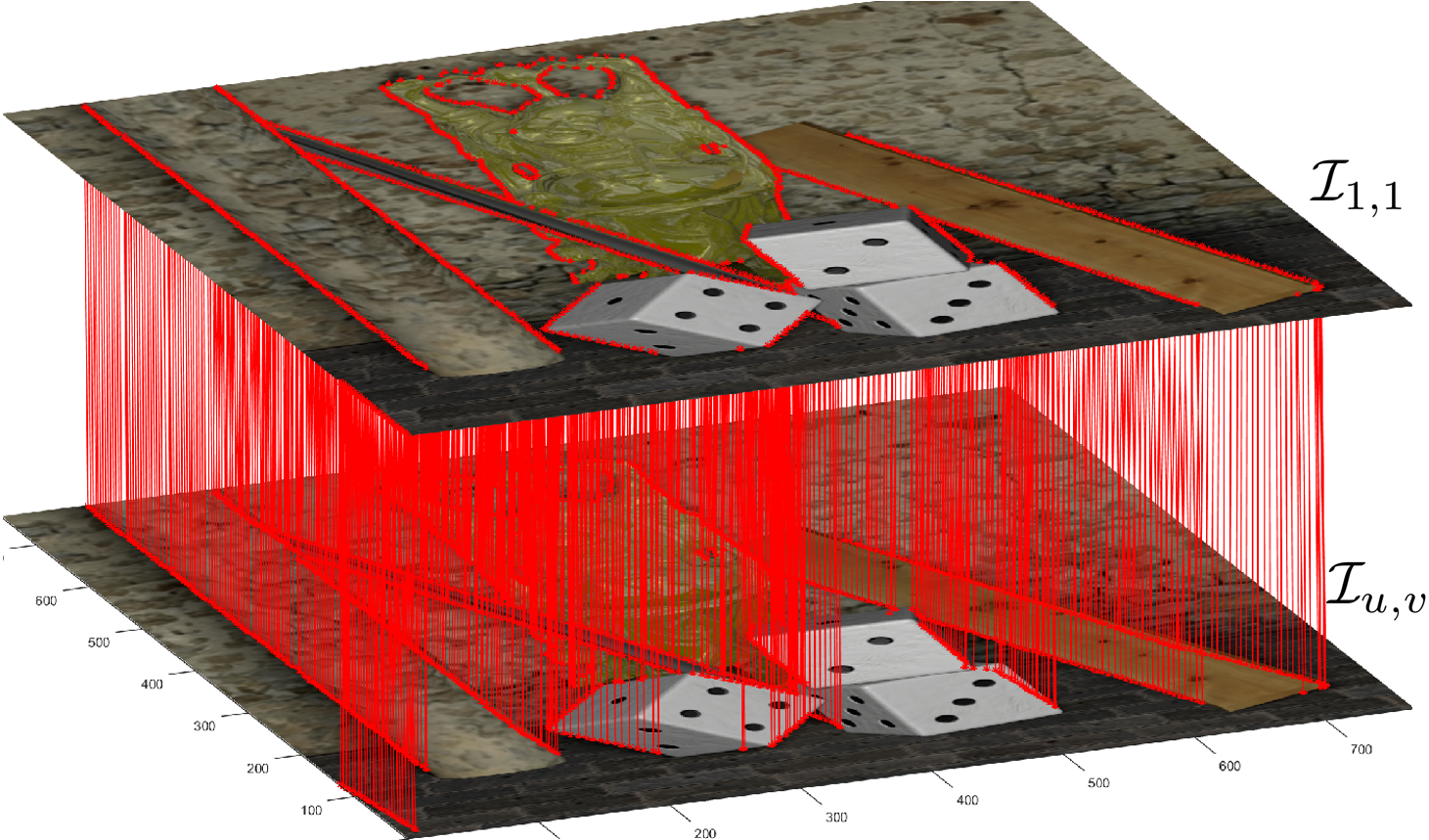
The graph connections are derived from the disparity and hold just enough information to synthesize other sub-aperture images from one reference image of the LF. Based on the concept of epipolar segment, the graph connections are sparsified (less important segments are removed) by a rate-distortion optimization. Fig. 1.(c) gives an illustration of the kept graph connections between I1,1 and Iu,v.

To enhance the quality of the reconstructed views, residues between a subset of M rendered images (from the graph) and the original true images are added to the graph. At the decoder, these selected sub-aperture images are also treated as “reference images” to render the remaining sub-aperture images. The depth of each straight segment in the reference image is estimated from the corresponding graph connections. Then, the depth of the selected images is computed by projection from the estimated depth of the reference view. We compute each remaining sub-aperture image by combining (M+1) rendered images, one image recovered from the graph and M images warped from the selected reference images.




(a) GBR for light field

(b) Example of graph connections between two views.

(c) Graph connections between two views.

Fig.1. Graph based representation (GBR) adapted to light fields

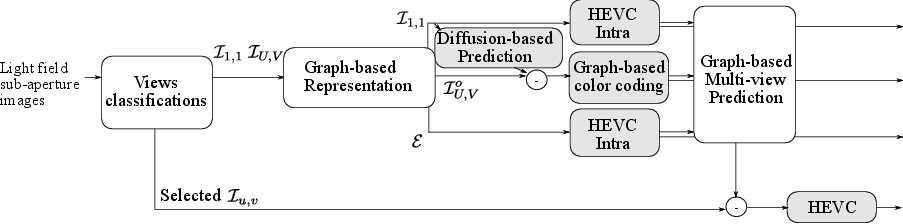
Coding Scheme

Fig.2. Proposed encoder
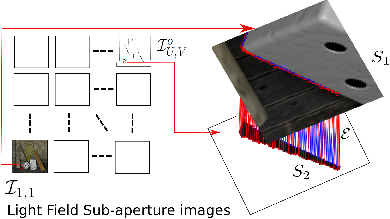
The graph edges E are stored in a grey-level image which is coded using HEVC. The vertices are pixels in the images I1,1 and IoU,V (the parts of IU,V that do not appear in I1,1). A part of the graph is depicted in Fig. 3 where blue segments are edges with a small weight (0.5) whereas red ones are edges with high weight (1). While I1,1 is classically compressed using HEVC, the arbitrarily shaped IoU,V requires dedicated tools. We propose to compress it using the weighted Graph Fourier Transform (wGFT) [6]. The residuals of the selected “reference views” are also compressed with HEVC.

Fig.3. Connections of the disoccluded pixels.

Results

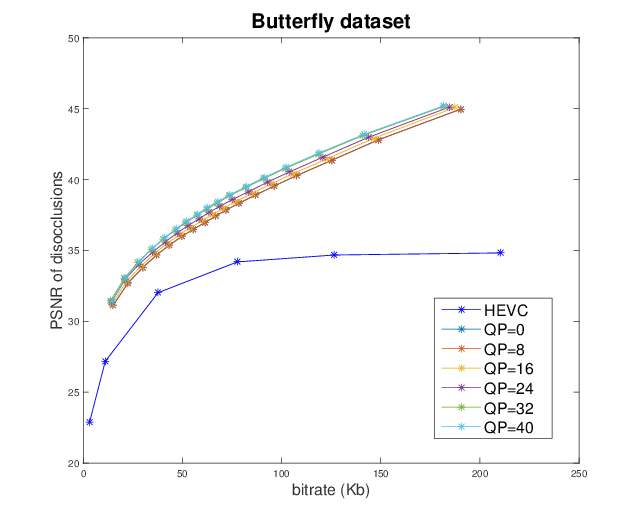
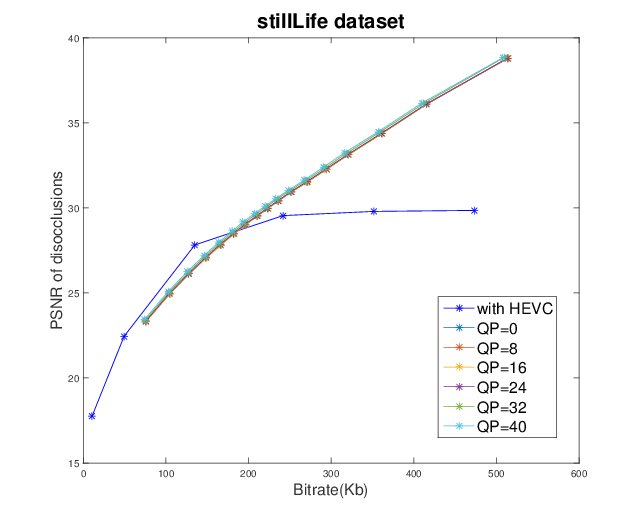
Evaluation of GFT

To show the interest of exploiting inter-view neighboring relations(i.e graph edges) in coding the disocclusions, we first compare the performance of our graph-based compression scheme against HEVC inter-coding. We first code the disoccluded parts along with the reference view as a video sequence using HEVC. We vary the QP from 0 to 40. For each QP, a prediction of the disocclusions is computed(Sec. 4), then the residuals are coded while varying the quality factor from 10 to 90. The bitrate is the one needed to code the disocclusions. The PSNR is measured taking as refer ence the original disocclusions color values. From the follwing results, we notice that our approach outperforms HEVC with a higher PSNR for most QP values while preserving acceptable bitrates. Our diffusion method yields a good predictionwith Buddha since the background mostly consists of smooth regions, and that explains the better coding performance. Whereas for monasRoom, the background is made of texture and wrong color values are propagated to the disoccluded areas resulting in residuals harder to code. The compression performances are assessed against those obtained by applying HEVC-based inter-coding on the sequences of images formed by extracting the sub-apertures images following a lozenge scan order starting at the central view.


buddha


butterfly


stillLife


monasRoom

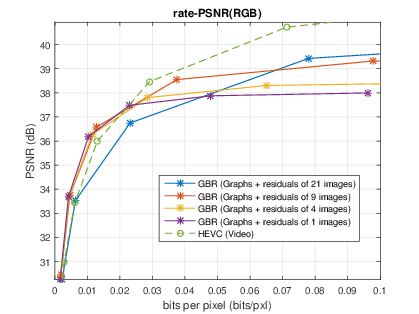
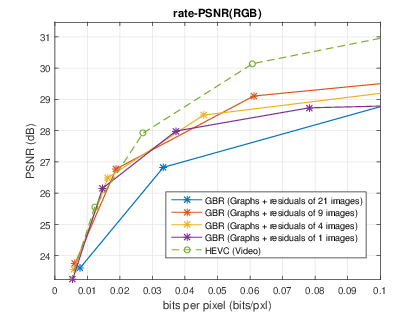
Light field representation and compression

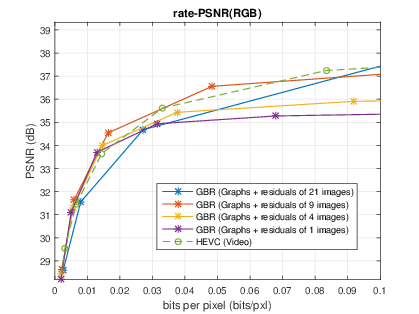
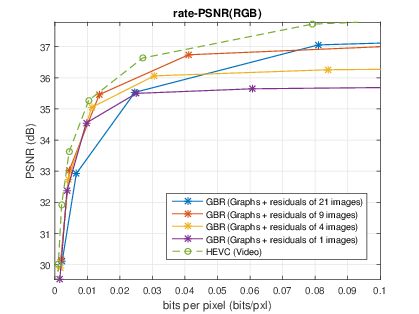
The number of sub-aperture images selected to add residuals is chosen as {1,4,9,21} with a regular sub-sampling pattern. The baseline method is the scheme which directly compresses the whole LF dataset as a video sequence with HEVC. At low bitrate, the proposed GBR can yield PSNR-rate gain. However, at high bitrate, the GBR scheme is outperformed by HEVC, due to the limited number of selected sub-aperture images.


buddha


stillLife


monasRoom


butterfly





GBR

Original

HEVC


GBR: 36.21dB with 0.011bpp; HEVC: 35.99dB with 0.013bpp



GBR: 34.94dB with 0.0111bpp; HEVC: 35.27dB with 0.0104bpp



GBR: 26.15dB with 0.0147bbp; HEVC: 25.57dB with 0.0123bpp



GBR: 33.94dB with 0.0142bpp; HEVC: 33.65dB with 0.0144bpp

References

[1] Sven Wanner, Stephan Meister, and Bastian Goldluecke, “Datasets and Benchmarks for Densely Sampled 4D Light Fields,” in VMV. Citeseer, 2013, pp. 225–226.

[2] Blender, “Blender,” https://www.blender.org/, [Online].

[3] Thomas Maugey, Antonio Ortega, and Pascal Frossard, “Graph-based representation for multiview image geometry,” IEEE Transactions on Image Processing, vol. 24, no. 5, pp. 1573–1586, 2015.

[4] Xin Su, Thomas Maugey, and Christine Guillemot, “Rate-Distortion Optimized Graph-Based Representation for Multiview with Complex Camera Configurations,” IEEE Trans. on Image Processing, submitted, 2017.

[5] Xin Su, Thomas Maugey, and Christine Guillemot, “Graph-based representation for multiview images with complex camera configurations,” in Image Processing (ICIP), 2016 IEEE International Conference on. IEEE, 2016, pp. 1554–1558.

[6] David I Shuman, Sunil K Narang, Pascal Frossard, Antonio Ortega, and Pierre Vandergheynst, “The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains,” IEEE Signal Processing Magazine, vol. 30, no. 3, pp. 83–98, 2013.