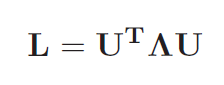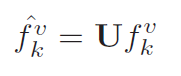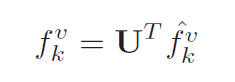Graph-based
Transforms for Predictive Light Field Compression based on
Super-Pixels
|
|
M. Rizkallah, X. Su, T. Maugey, C. Guillemot,
"Graph-based Transforms for Predictive
Light Field Compression based on Super-Pixels", IEEE
International Conference on Acoustic, Speech and Signal Processing
(ICASSP), Calgary, 15-20 Apr. 2018.(pdf)[change]
|
Abstract
In
this paper, we explore the use of graph-based transforms to capture
correlation in light fields. We consider a scheme in which view
synthesis is used as a first step to exploit inter-view correlation.
Local graph-based transforms (GT) are then considered for energy
compaction of the residue signals. The structure of the local graphs
is derived from a coherent super-pixel over-segmentation of the
different views. The GT is computed and applied in a separable manner
with a first spatial unweighted transform followed by an inter-view
GT. For the inter-view GT, both unweighted and weighted GT have been
considered. The use of separable instead of non separable transforms
allows us to limit the complexity inherent to the computation of the
basis functions. A dedicated simple coding scheme is then described
for the proposed GT based light field decomposition. Experimental
results show a significant improvement with our method compared to
the CNN view synthesis method and to the HEVC direct coding of the
light field views [3].
Datasets
We
test our GBR on four Real Light Fields [ref] (9x9 views of 536x376
pixels): Flower1, Flower2, Cars and Rock.
Light
Field Predictive Coding Scheme
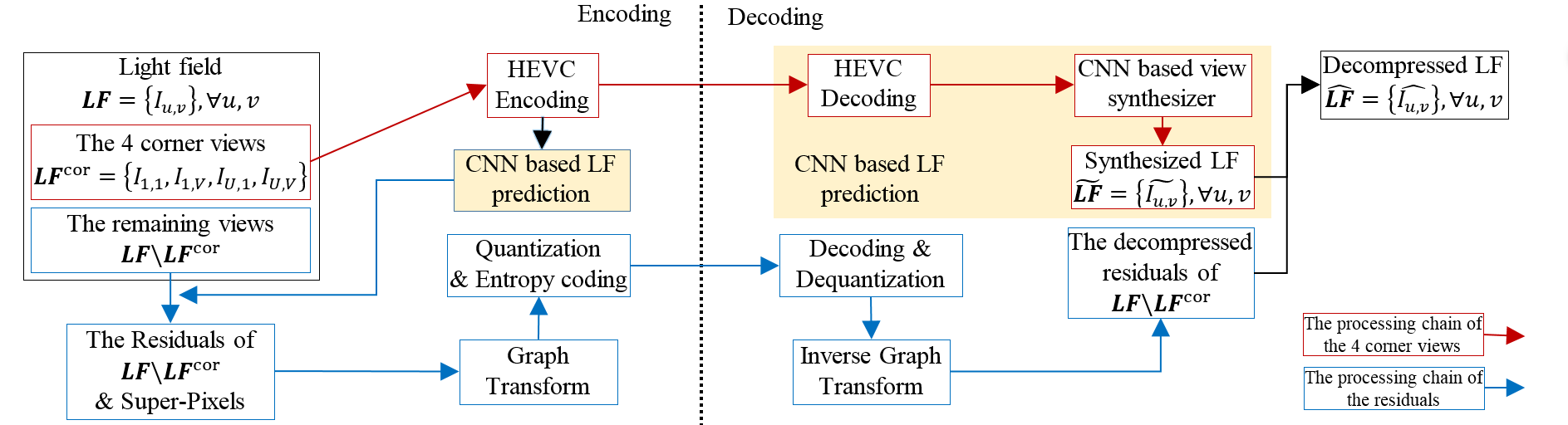
Fig.2.
Proposed encoder
Fig.
2 depicts the proposed coding scheme. Let LF={Iu,v}
denote a light field, where u=1,...,U and v=1,...,V are the view
indices. Four views at the corners LFcor={I1,1
,I1,V ,IU,1 ,IU,V} are encoded using
HEVC-Inter and used to synthesize the whole light field with the CNN
based synthesis method [1], as shown in Fig. 2 (red arrows). To
improve the quality of the synthesized light field, the residuals
between the synthesized and original views are encoded using graph
transforms, (see Fig. 2, blue arrows). The residuals of all the views
but the 4 corner views LF\LFcor
are considered here. These residual signals are grouped into
super-pixels using the SLIC algorithm [2], then graph transforms are
applied on each super-pixel followed by quantization and entropy
coding. At the decoder, the decompressed residuals are added to the
synthesized light field to obtain the final decompressed light field.
Graph-based
Transforms and Coding
Thanks
to the superpixel ability to adhere to image borders, the
sub-aperture residual images are subdivided into uniform regions
where the residual signal is supposed to be smooth. Fig. 3(c) shows
the luminance values of a cropped region of the residues for a subset
of views of the Flower 1 dataset. Although the disparity is not taken
into account, the signals in super-pixels which are co-located across
the views are correlated for light fields with narrow baselines. In
order to capture these correlations, we use a separable Graph
Transform comprising a local super-pixel based spatial GT followed by
a local angular GT.
First
Spatial GT:
We
first construct local spatial graphs inside each super-pixel for each
view. We then use the Laplacians of the graphs to define a first
spatial Graph transform. Since the Laplacian is positive
semi-definite, it has a complete set of eigenvectors as:
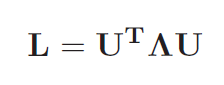
Using
the matrix U
where rows are eigenvectors, the transformed coefficients vector is
defined in [4] as:
The
inverse graph Fourier transform is then given by:
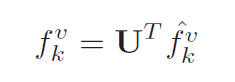
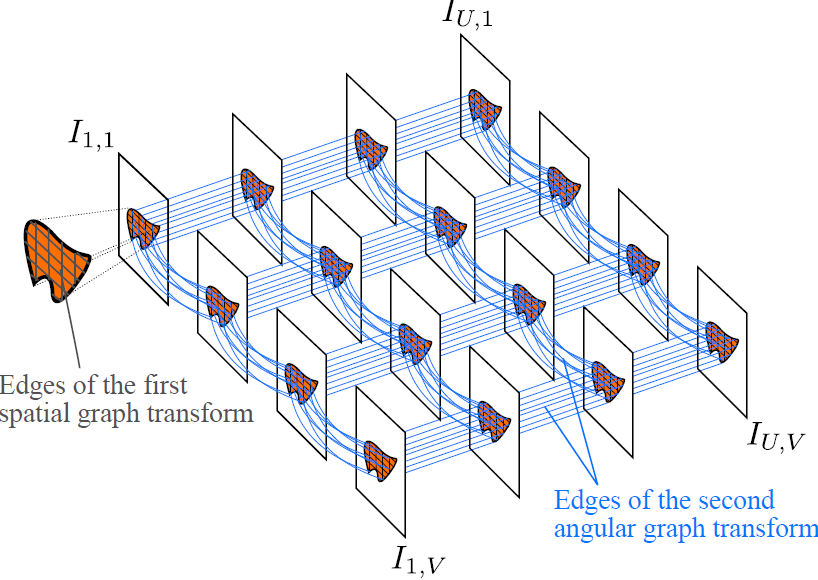
Second
angular GT:
In
order to capture inter-view dependencies and compact the energy into
fewer coefficients, we perform a second graph based transform. Since
we have the same number of pixels for a specific super-pixel in all
the views, we then deal with a graph made of Nv vertices
corresponding to the views to be coded. Edges are drawn between each
node and its direct four neighbors. We examine two different cases
where the weights are either fixed to 1 or learned from a training
set of spatial transformed coefficients [5]. We refer to those two
versions as unweighted GT (uGT) and weighted GT (wGT).
|

(a)
Original view of Flower1
|

(b)
Superpixel segmentation
|
|
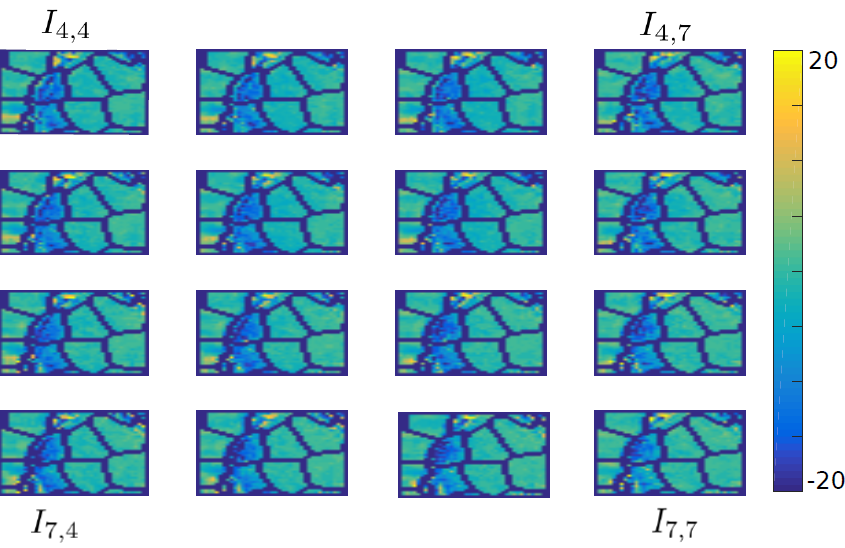
(c)
Coherent superpixels across views
|

(d)
Illustration of the two graphs drawn to compute separable
graph
based transforms
|
Fig.
3 Super-pixels and Graph Transforms
Coding
of transform coefficients:
At
the end of those two transform stages, coefficients are grouped into
a three-dimensional array R where R(iSP,ibd,v)
is the vth transformed coefficient of the band ibdfor
the superpixel iSP. Using the observations on all the
superpixels in a training dataset, we can find the best ordering for
quantization. We first sort the variances of coefficients with enough
observations in decreasing order. We then split them into 64 classes
assigning to each class a quantization index in the range 1 to 64.
All the remaining coefficients with less observations will be
considered in the last group. We use the zigzag ordering of the JPEG
quantization matrix to assign the quantization step size for each.
The quantized coefficients are further coded using an arithmetic
coder.
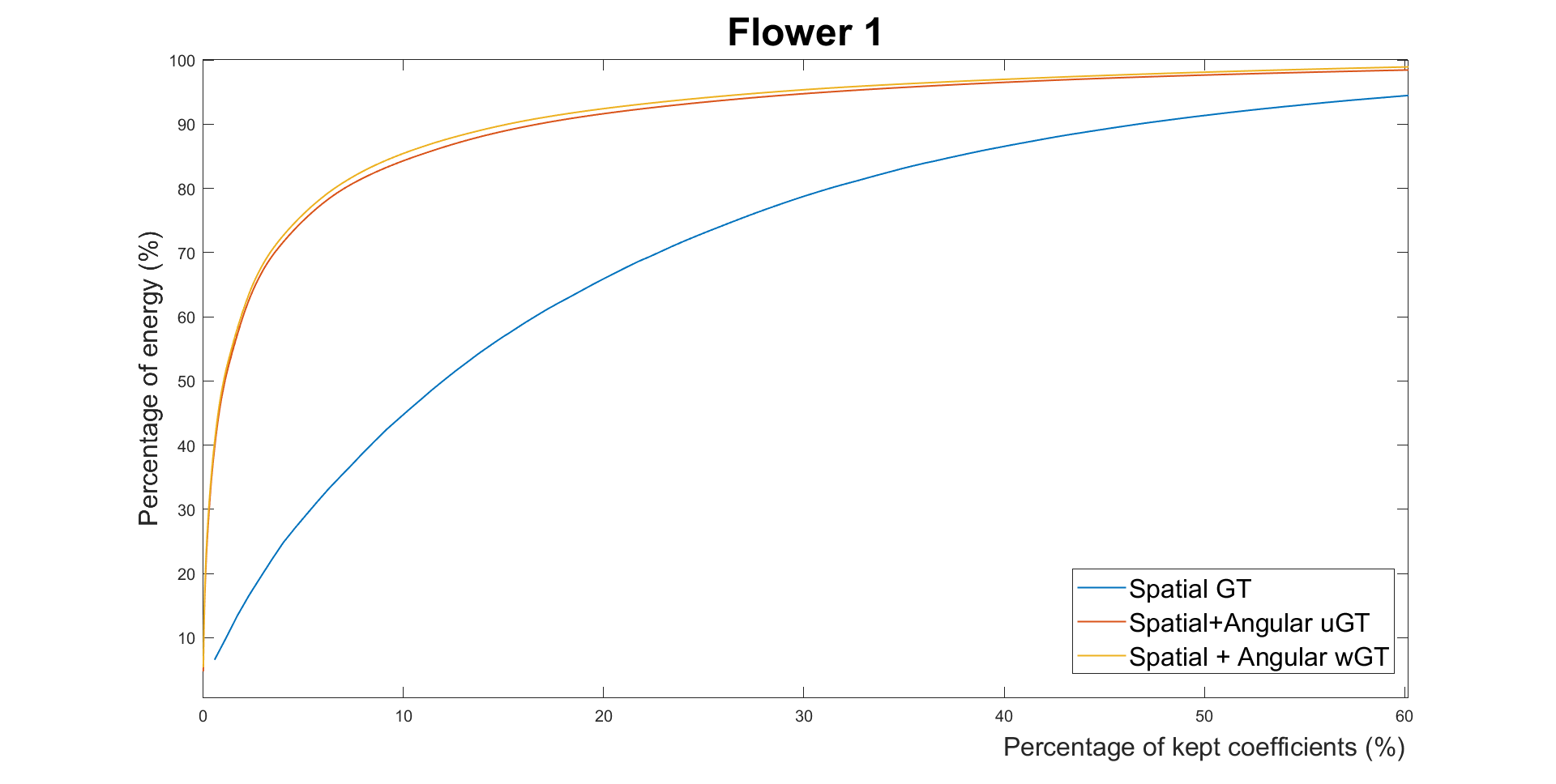
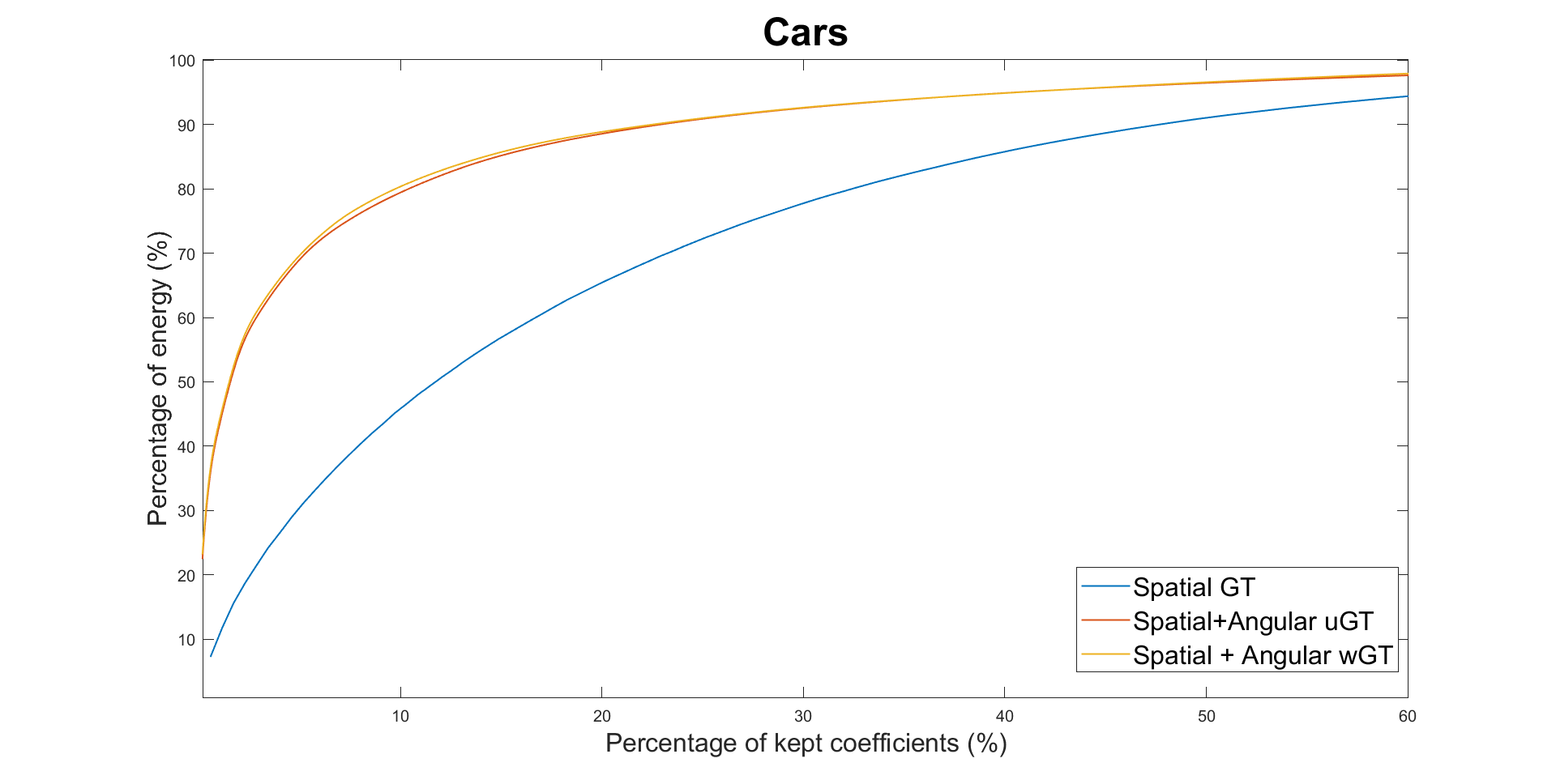
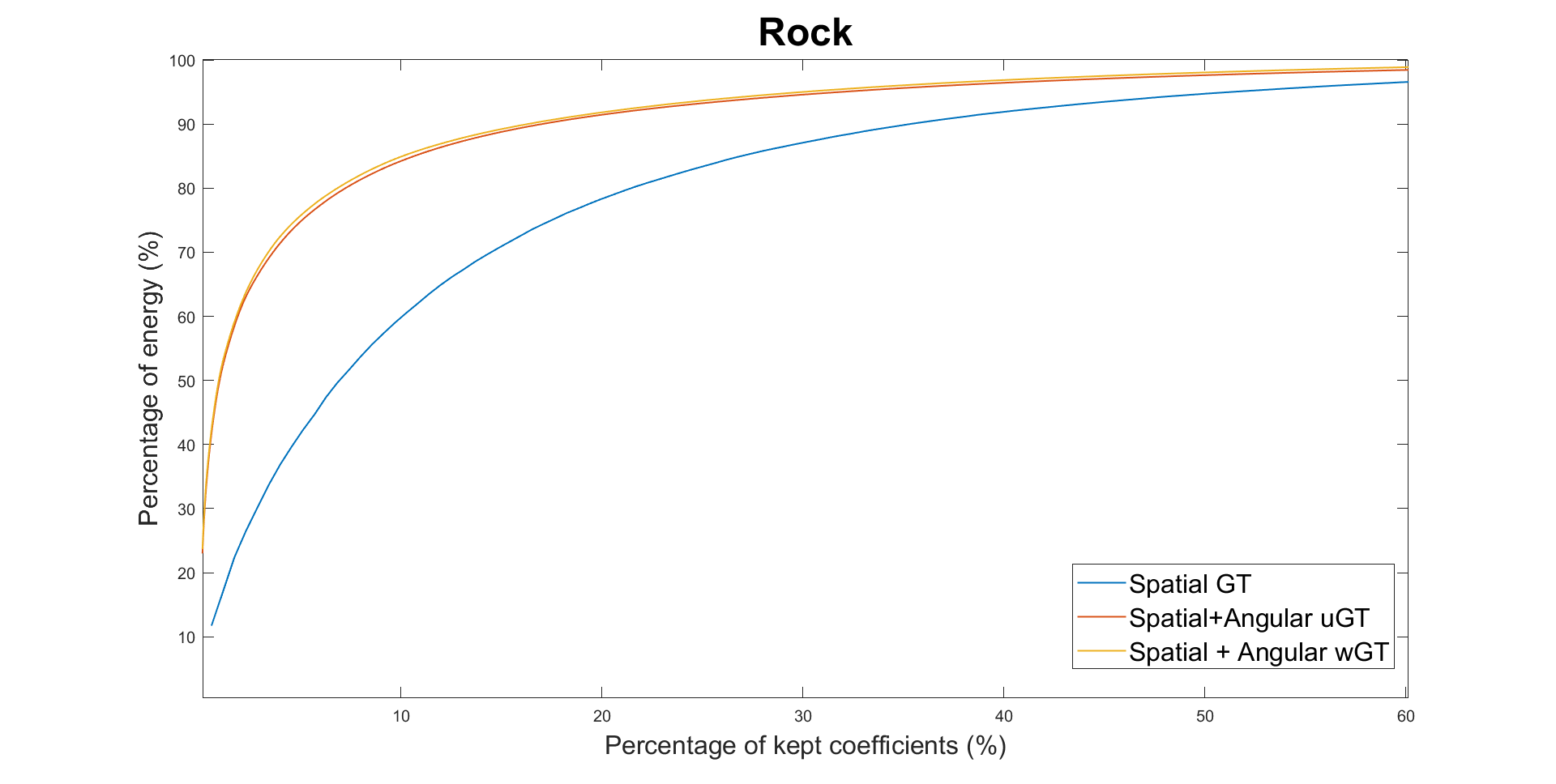
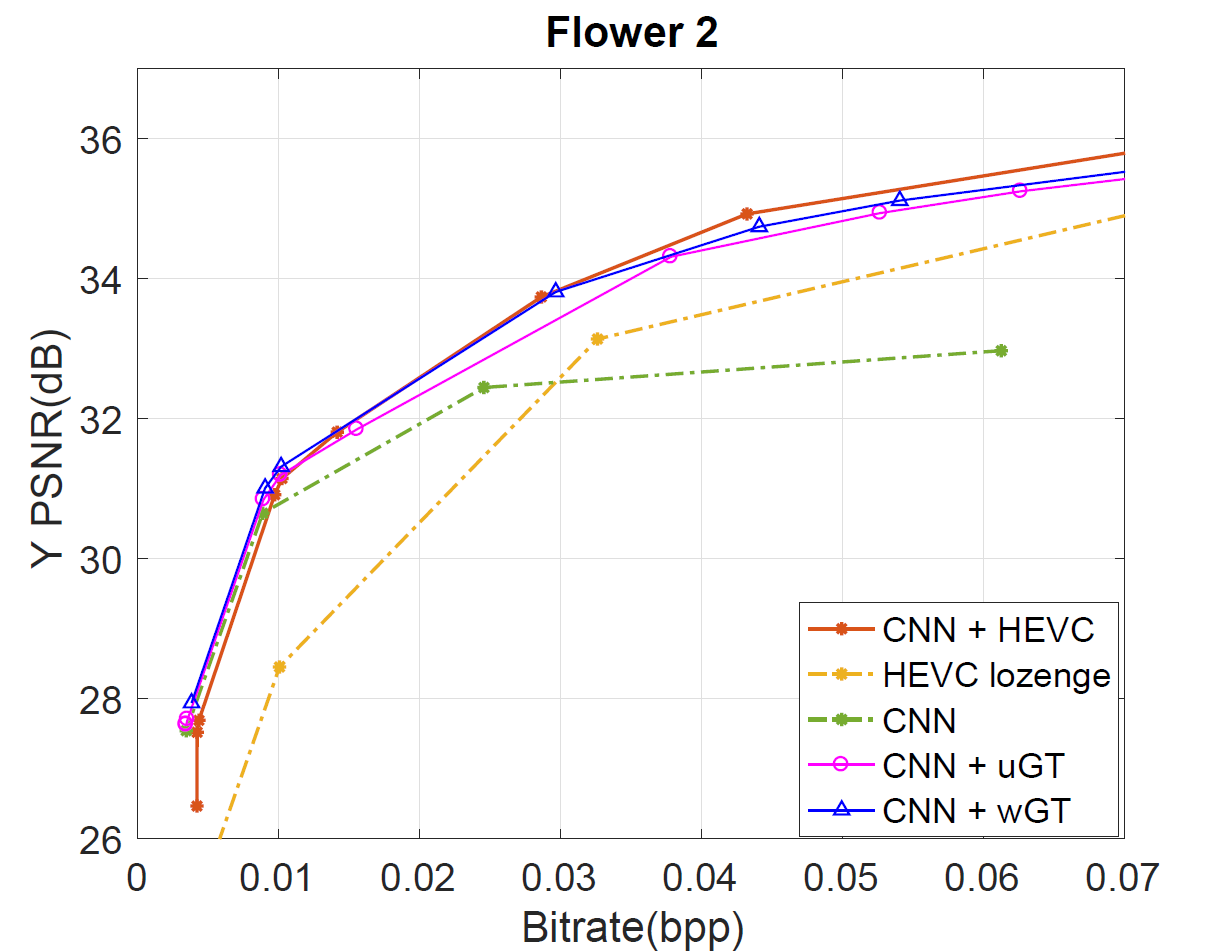
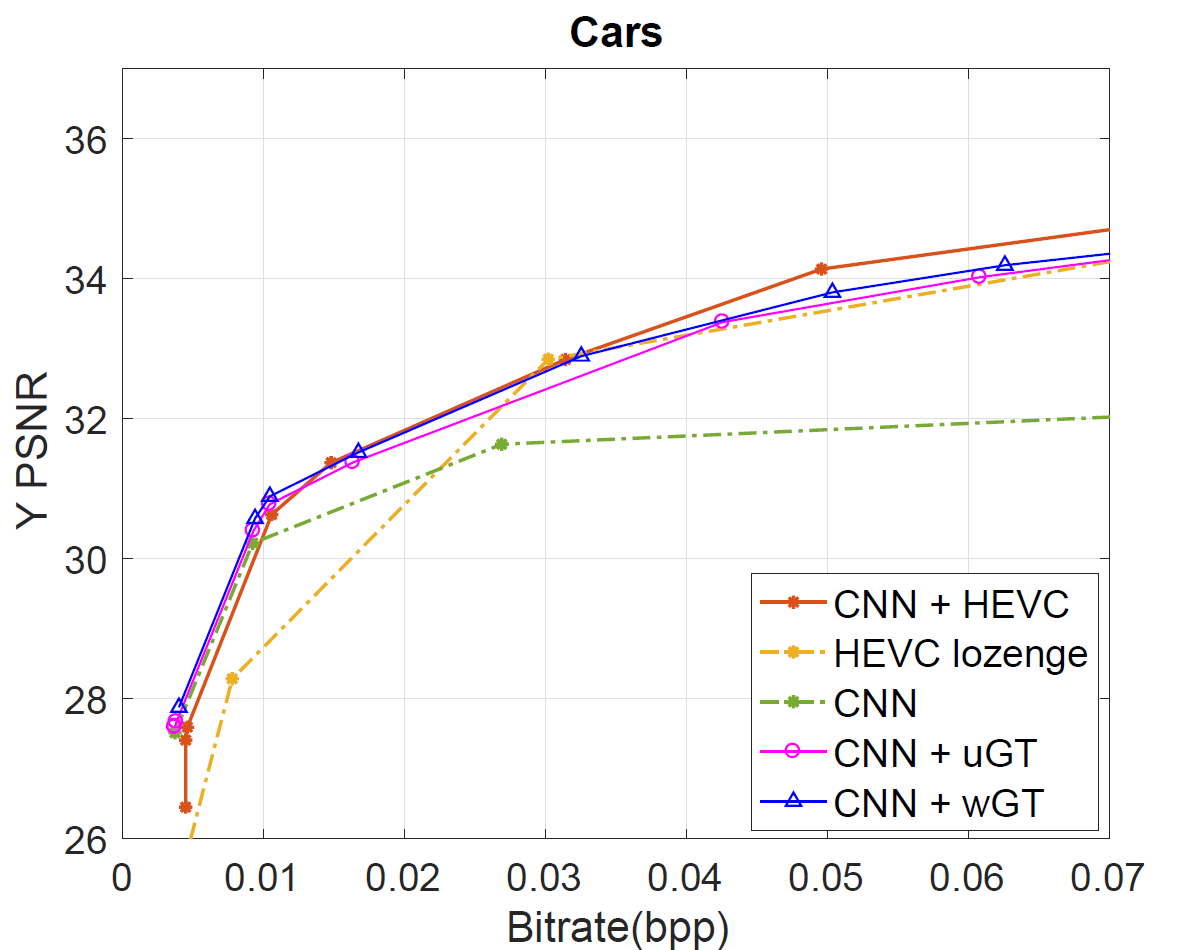
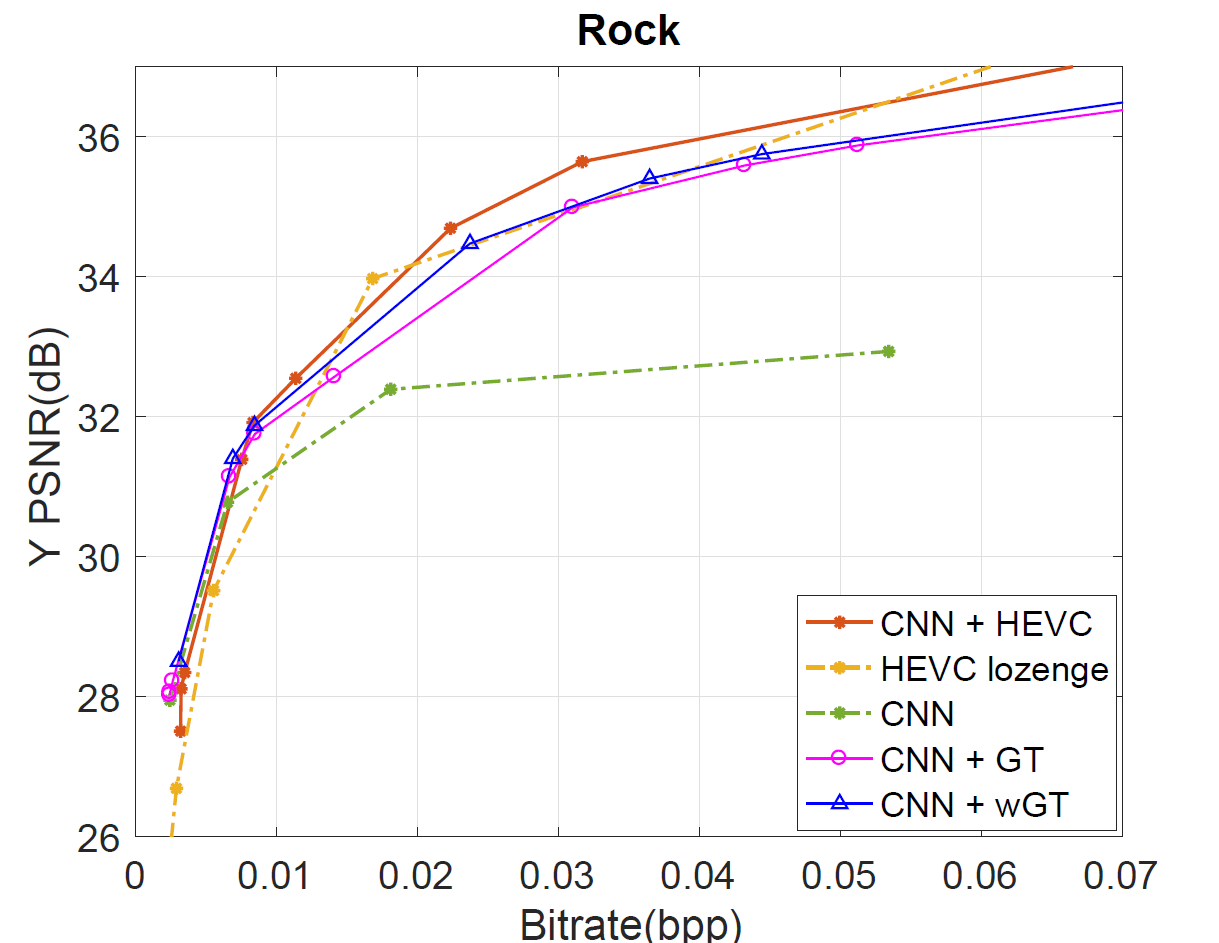
Results
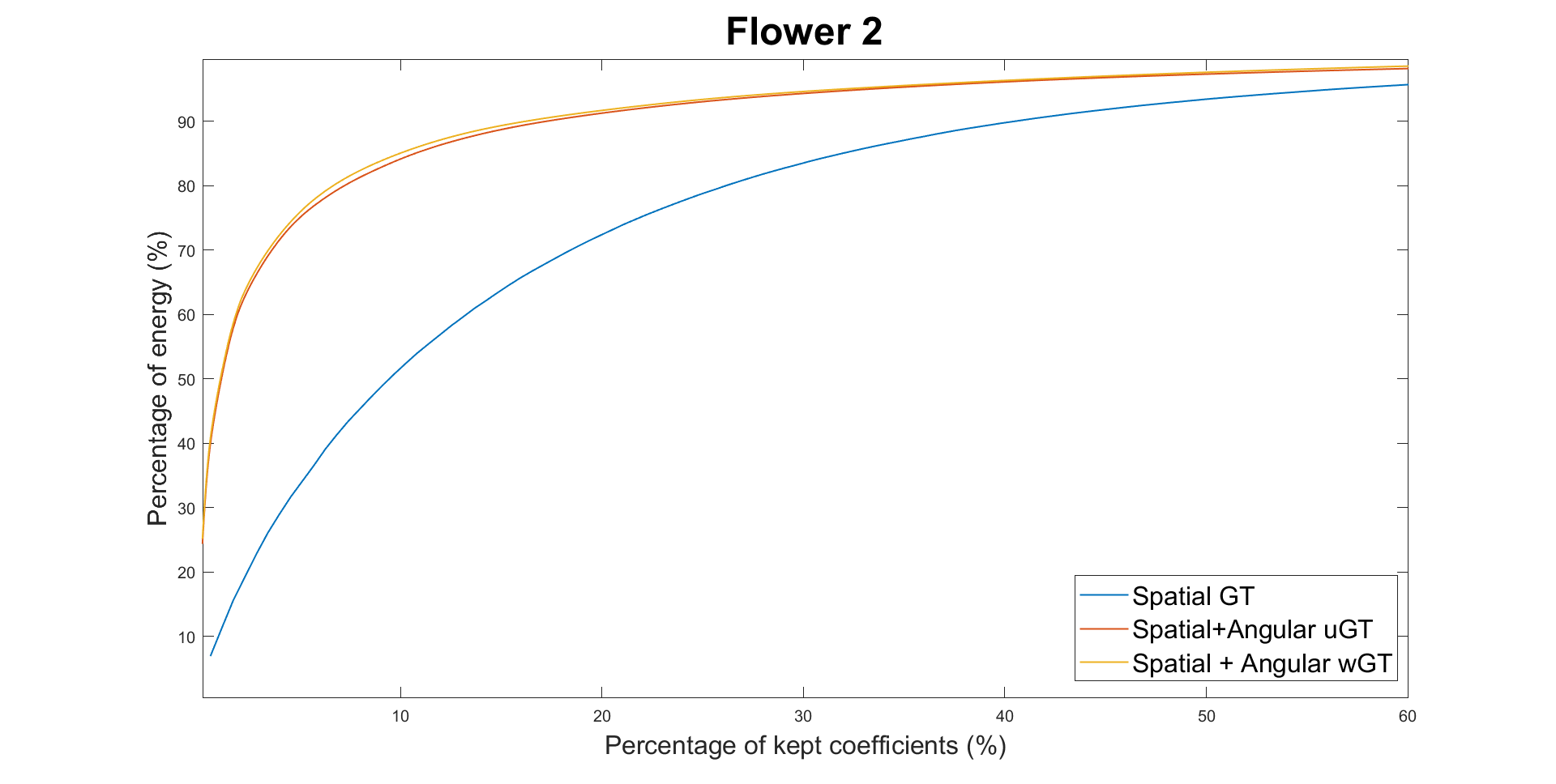
We
first evaluate the energy compaction of the transformed coefficients
for the three transforms (only spatial GT, spatial + unweighted
angular GT, spatial + weighted angular GT) to show the utility of
exploring inter-view correlation. Results for the four datasets are
shown in the Fig. 4. Higher energy compaction is observed with the
second angular transform compared with only applying the spatial
transform, with a slight improvement for the wGT. This shows the
utility of exploring the inter-view correlations between residues in
different views and adapting the graph weights for that purpose
compared to only performing local spatial transforms.
Energy
compaction
Rate-distortion
Evaluation
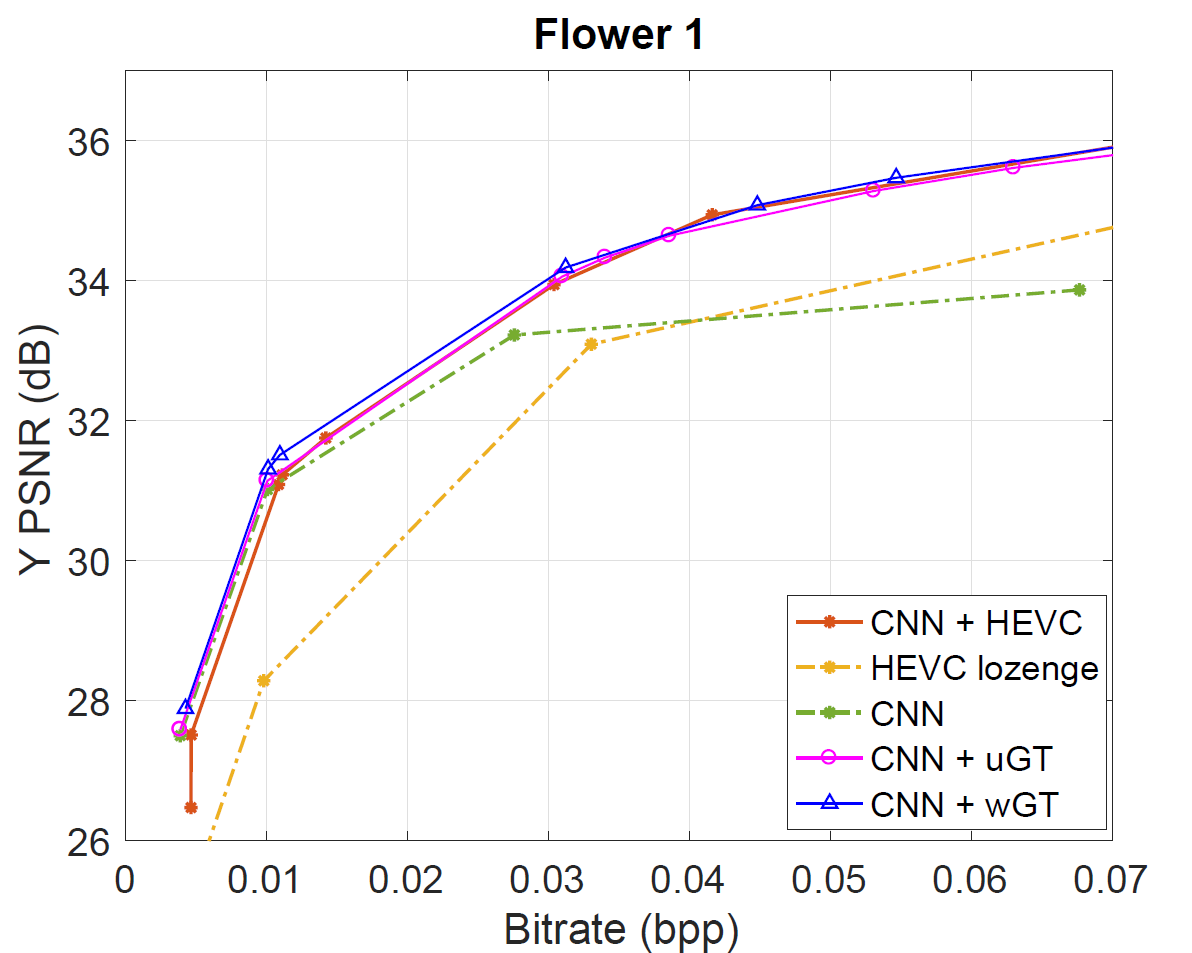
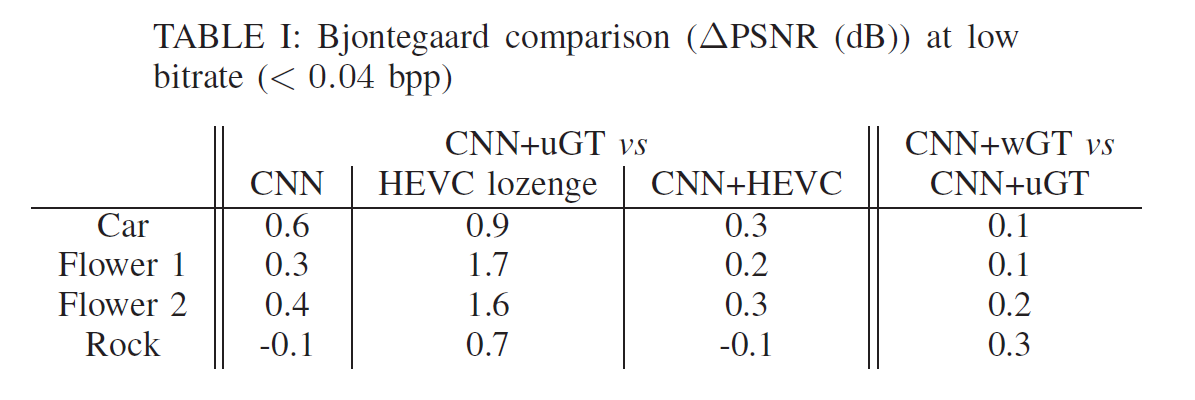
For
the four datasets, our Graph based transform approaches defined by
CNN+uGT and CNN+wGT slightly outperform CNN learning based scheme at
low bitrate and bring a small improvement to the HEVC based coding of
the residues. For higher bitrates, the compression performance is
further enhanced compared to CNN, and almost reaching CNN+HEVC
performance. At low to middle bitrates, both graph-based transform
schemes outperform direct use of HEVC inter coding as we can also
observe after computing the bjontegaard metric in Table I.
References
[1]
N.
K. Kalantari, T.-C. Wang, and R. Ramamoorthi. Learning-based view
synthesis for light field cameras. ACM
Transactions on Graphics
(Proceedings
of SIGGRAPH Asia 2016),
35(6), 2016
[2]
R.
Achanta, A. Shaji, Kevin K. Smith, A. Lucchi, P. Fua, and S.
Susstrunk. SLIC Superpixels Compared to State-of-the-Art Superpixel
Methods. IEEE
Trans. Pattern Anal. Mach. Intell.
[3]
M.
Rizkallah, T. Maugey, C. Yaacoub, and C. Guillemot. Impact of light
field compression on focus stack and extended focus images. In 24th
European
Signal
Processing Conf. (EUSIPCO),
pages 898–902, Aug. 2016.
[4]
David I Shuman, Sunil K Narang, Pascal Frossard, Antonio Ortega, and
Pierre Vandergheynst, “The emerging field of signal processing
on graphs: Extending high-dimensional data analysis to networks and
other irregular domains,” IEEE
Signal Processing Magazine,
vol. 30, no. 3, pp. 83–98, 2013.
[5]
H.
E. Egilmez, E. Pavez, and A. Ortega. Graph learning from data under
laplacian and structural constraints. IEEE
Journal of Selected Topics in
Signal
Processing,
11(6):825–841, Sept 2017.